时间交织ADC的基本数学原理和校准方法
本文总结了时间交织ADC的基本数学原理和校准方法。
时间交织ADC的频域分析
在时间交织ADC中,将原先单通道的,以$f_s$为采样频率的采样工作,被均匀分配给N个通道交替完成。因此,N个通道交替完成采样频率为$f_s$的采样工作,每个通道上的频率变为原先的$\frac{1}{N}$。
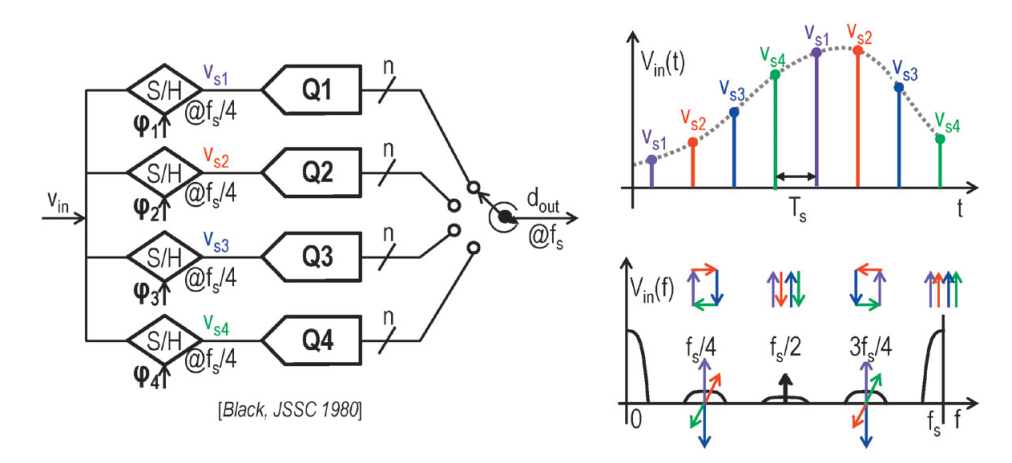
如图所示该时间交织中一共有4个通道,通道1至通道4分别用紫色、红色、蓝色以及绿色表示。根据时域中的移位对应于频域中的移位
$$
y_1(t)=x(t)\Sigma(\delta (t-kT_{ck}))
$$
$$
y_2(t)=x(t)\Sigma(\delta (t-kT_{ck}+\frac{T_{ck}}{4}))
$$
$$
y_3(t)=x(t)\Sigma(\delta (t-kT_{ck}+\frac{2T_{ck}}{4}))
$$
$$
y_4(t)=x(t)\Sigma(\delta (t-kT_{ck}+\frac{3T_{ck}}{4}))
$$
$$
Y_1(f)=\frac{1}{T_{ck}}X(f)*\Sigma(\delta (f-kf_{ck}))
$$
$$
Y_2(f)=\frac{1}{T_{ck}}X(f)*\Sigma(\delta (f-kf_{ck})e^{-j\pi fT_{ck}/2})
$$
$$
Y_3(f)=\frac{1}{T_{ck}}X(f)*\Sigma(\delta (f-kf_{ck})e^{-j\pi fT_{ck}})
$$
$$
Y_4(f)=\frac{1}{T_{ck}}X(f)*\Sigma(\delta (f-kf_{ck})e^{-j3\pi fT_{ck}/2})
$$
根据上式可以发现,每一个通道的频谱都是在通道一的基础之上进行一定的相移;而通道一来自于包络函数的傅里叶变换按照采样频率进行周期为采样频率的周期延拓。
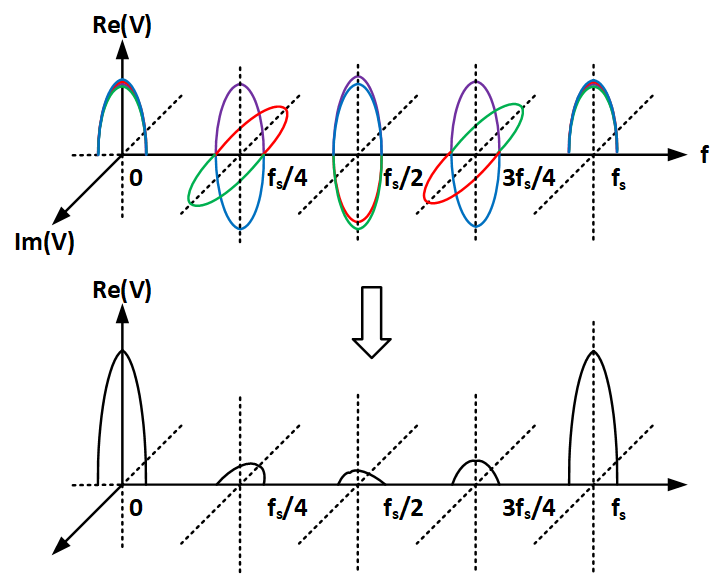
考虑离散谱时,即采用离散傅里叶变换(DFT)时,不仅该信号的时域表达式离散化,该信号的频域表达式也离散化,这就会导致该信号的时域表达式周期化,即该信号需要在原有信号基础之上进行若干点的周期延拓。举例来说,如果原信号的离散序列一共有N个值,对该信号做N点DFT,则原信号需要进行以N个样本点为周期的周期延拓。
$$
X(f)=\frac{1}{N}\Sigma x(n)e^{j2\pi nf/N}
$$
上式表述了N点离散傅里叶变化的表达式,注意到,在该表达式中,我们有求累加和之后除以系数N,这是由于傅里叶变换本身的物理意义导致的。傅里叶变换的到的频谱函数$X(f)$得到的频谱表达式的模表示了幅度,而模的平方表示了功率。假如系数$\frac{1}{N}$没有被考虑在表达式中,则会出现一个奇怪的现象,那就是点数越多,离散傅里叶变换得到的表达式的模值就会越大,自然模的平方也就会越大,这和实际的物理意义是相悖的,我们知道,信号的功率不会因为采样点数目的增大而增大。为了解决这个问题,我们在离散傅里叶正变换的等式右边加上一个系数$\frac{1}{N}$,这样就能保证不管采样点数如何改变,得到的信号的功率谱的模值总是不变的。
但是在时间交织ADC中,假设通道数由单通道变为双通道的ADC,对于整体而言,采样率变为原先的2倍,对于双通道ADC的一个通道而言,相当于在原先单通道的基础之上,在中间插入了一个0值,根据我们前面的论述可知,通道1的功率变为了原先单通道的一半,信号幅度变为原先的0.707倍;因为该ADC有两个通道,所以加起来的总功率仍然保持不变。
在ADC中,由失配引起的杂散(Spurs)是ADC需要关注的重要的问题,关系到ADC的性能。假设每一个通道的失配的比例是固定的,是一个分布确定的随机变量,假设这个比例的数学期望是0,方差是$\sigma^2$。
举一个单通道和双通道的失配例子,假设单通道的失配随机变量是$e$,双通道的失配随机变量是$e_1$和$e_2$。为了求得失配的功率,我们可以将每一个变量的失配比例求和之后取数学期望后平方,获得功率。由下面的式子可以知道,单通道ADC的杂散幅度是双通道的ADC杂散幅度的$\sqrt{2}$倍。在这里提醒读者,这里说的双通道特别强调了是杂散幅度,而不是总共的杂散功率,总的杂散功率还需要乘以一个通道数。
$$
E(e)^2=E(e^2)=\sigma^2
$$
$$
E(\frac{e_1}{2}+\frac{e_2}{2})^2=E((\frac{e_1}{2})^2)+E((\frac{e_2}{2})^2)=\frac{1}{2}\sigma^2
$$
因此,不难看出,不管是单通道还是双通道还是N通道,只要信号包络保持不变,杂散的总功率是保持不变的,但是在每一个通道上的杂散幅度会变小,具体来说,会下降为原先幅度的$1/\sqrt{2}$,也就是下降3dB,而功率保持不变。
时间交织ADC的频域分析的MATLAB验证
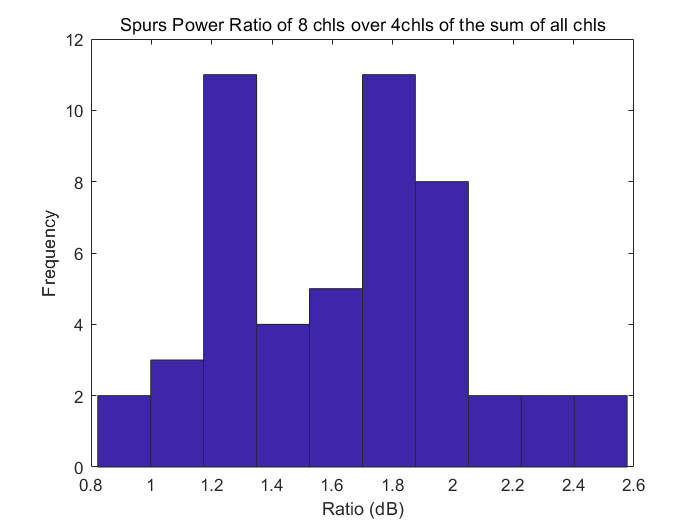
为了证明上述结论的正确性,这里我们在MATLAB中给四通道和八通道ADC建立了模型,验证了结果的正确性。我们令失配随机变量是一个服从正态分布的随机变量,将这个失配变量叠加在每一个通道上,之后,测量100次在这个随机变量的影响下,八通道ADC的杂散幅度大小与四通道的杂散幅度大小的比值,测定结束之后将该值存储在数组中。将上述步骤反复执行50次,得到了一份概率分布图,可以看到,该均值大概在$1/\sqrt{2}$附近,也是3dB附近,可以验证我们之前的结论:n通道ADC的杂散幅度是2n通道的ADC杂散幅度的$\sqrt{2}$倍。
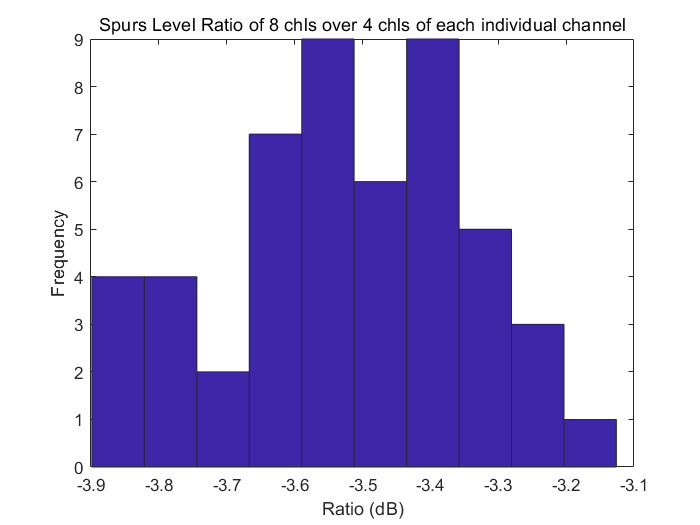
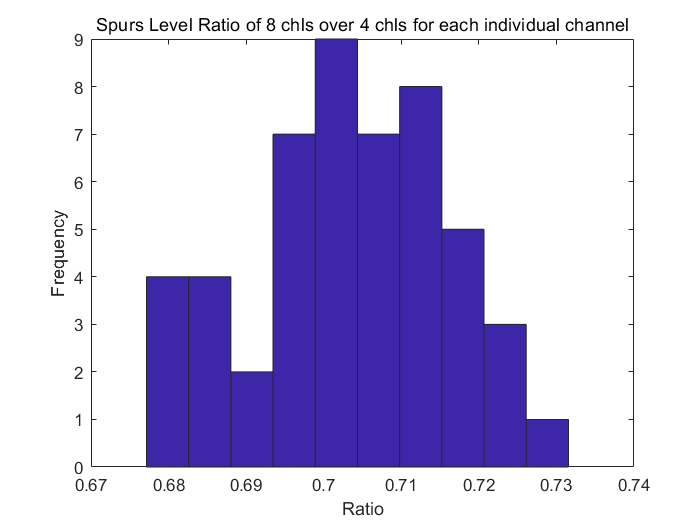
再来验证是否杂散总功率保持不变,下面给出了按照上文所述流程测量出来的杂散功率比值,我们可以看到,8通道与4通道ADC的杂散功率比值在1.5附近,此比例大概是1.2左右,这里的杂散功率并没有完全相等的原因不甚明确,需要进一步讨论和研究。
结论
我们可以看到,在时间交织ADC中,在不考虑电路层面的误差仅仅考虑失配的前提下,每增加2倍的通道数量,杂散的幅度就会降低3dB,因此,增加时间交织通道数目可以显著减小杂散的幅度。但是,依据数学计算结果,无论通道数如何增加,杂散的总功率保持不变。
TI失调失配来源与校准方案
TI的失调失配主要来源于比较器,失调失配在输出主要体现为一个单音信号或者多音信号,对于每一个通道来说,我们认为失调在某一段时间内是恒定不变的;并且在输入为零时进行校准,这样只需要将输入一段时间内的数据进行累加求平均之后即可得到最后的失调量,具体来讲可以通过下面的系统框图看到。

该系统框图的传输函数可以表示为如下图所示的表达式,
$$
\frac{V_{out}}{V_{in}}=\frac{A}{1+A}=\frac{1/s}{1+1/s}=\frac{1}{1+s}
$$
从上式中可以看出,该系统表现为一个低通的特性,因此一些较为高频的信号会被滤除,因此只保留了低频的失调量信号。如果每一个通道都可以利用这样的一个系统框图进行失调量的估计的话,则可以获得每一个通道的失调量大小,进而在数字域对其进行补偿。
或者我们可以直接从Err中获得补偿过后的信号,Err的表达式如下式所示,
$$
\frac{Err}{V_{in}}=\frac{1}{1+A}=\frac{1}{1+1/s}=\frac{s}{1+s}
$$
可以看到,在上式中,在频率为DC处,信号被完全抑制,因此,在这个频率段处,我们可以获得滤除低频DC频段的信号,即一个去掉失调量的信号。上述失调失配预测&校准系统如果应用于一个4通道的校准系统中,则由于混叠造成的影响,在$\frac{fs}{4}$、$\frac{fs}{2}$、$\frac{3fs}{4}$、以及$fs$处会有信号的抑制作用,因此,如果想要降低这一部分抑制作用对系统带来的影响,我们需要将系统的3dB频点压缩到尽量靠近$\frac{fs}{4}$、$\frac{fs}{2}$、$\frac{3fs}{4}$、以及$fs$这几个点的位置,这样,即便输入宽带信号在这几个频点上有一定的能量损失,在整体上来看信号功率的损失仍然不算很大。
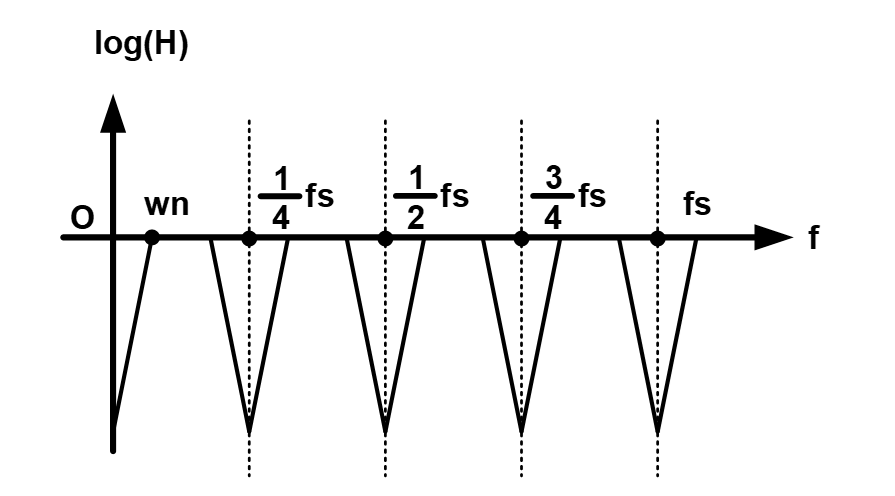
具体来说,上述功能可以通过在积分器上加上一个系数来实现,加上系数$\omega_n$之后的系统框图如下图所示。

该Err的表达式变为,
$$
Err=\frac{s}{s+\omega_n}
$$
该$\omega_n$的数值可以调节为一个比较小的数值,这样3dB频点就会非常靠近DC、$\frac{fs}{4}$、$\frac{fs}{2}$、$\frac{3fs}{4}$、以及$fs$。
TI增益失配来源与校准方案
TI增益的失配主要来源于传输线上的阻抗不匹配导致的,并且由于传输线上有可能是一个容性和感性的混合阻抗,因此,该阻抗有可能是一个输入信号频率的函数。那么,这种由于阻抗形成的增益失配也有可能是一个输入信号频率的函数,这就意味着如果考虑频率的情况下,系统的增益失配是一个很难校准的量。但一般来讲,这种频率的依赖性是可以通过布局布线进行削弱的,因此,我们在考虑这个问题的时候,只需要考虑一个恒定的增益失配即可。
在校准增益失配的时候,需要计算出一个增益系数,增益系数由下式表示,
$$
g_k=\frac{1}{N}\Sigma^{N-1}_{i=0}Q_k^2(i)
$$
上式中,$k$表示通道数,例如第$k$个通道,上述式子的实际含义是将每个通道的量化结果进行平方之后取均值。在得到这个增益系数之后,我们可以通过增益系数来校正增益误差,在下式中考虑一个四通道的TI-ADC,则第一个通道认为增益是准确的,其余通道校准到第一个通道的标准增益上。
$$
G_1=G_1
$$
$$
G_2=\sqrt{\frac{g_1}{g_2}}G_2
$$
$$
G_3=\sqrt{\frac{g_1}{g_3}}G_3
$$
$$
G_4=\sqrt{\frac{g_1}{g_4}}G_4
$$
利用上述的四个式子,即可以校准增益。下面的系统框图表示了上述的求增益系数的运算在电路当中实现的方法,可以使用寄存器对输入的信号进行N次寄存之后求和输出,便可以获得增益系数。

TI时钟失配来源与校准方案
TI中的时钟失配主要来源于时钟的非理想性,LC振荡器在产生高速时钟时会有一个抖动,这个抖动的$\sigma$在LC振荡器这种电路结构中最好可以做到$50fs$。另一方面,由于不同的信号通路,也会给时钟造成先后的时间差,这种时间差就造成了TI-ADC的多路时钟失配。随着输入信号的频率的增大,这种失配造成的噪声是越来越大的,这是由于频率增大意味着在单位时间内信号的变化就越大,造成的误差也就越大,进一步,噪声也就越大。因此,在高频应用中,这种失配造成的误差是必须要被校准的,否则会对系统的精度造成比较大的影响。
时钟失配校准的方法比较繁琐,接下来介绍这种基于自相关算法的时钟失配校准方法。假设我们采用了2路交织的ADC结构,这时,校准2路ADC时需要考虑基准的问题,时钟抖动是相对的,需要将某一个通道作为基准,将其他通道校准到以某一个通道为基准的周期上。下图描述了一个两通道的样本校准模型,可以看到1通道的样本将2通道的样本夹在了中间。如果2通道的样本向左移动,则$y_1[k-1]$与$y_2[k-1]$的相关程度会增加,$y_2[k-1]$与$y_1[k]$的相关程度会减小。
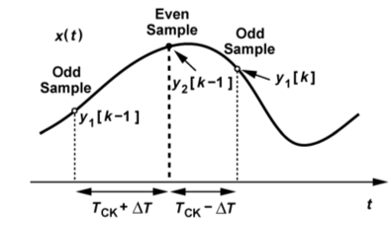
根据上述论述,我们可以发现,根据这个相关程度的大小关系,我们可以判断出中间的样本点究竟是偏向左边还是偏向右边。如果要从数学角度来表述上述分析过程,则所谓的相关程度可以表示为,
$$
P_1=x[-(T_{ck}+\Delta T)]x(0)
$$
$$
P_2=x(0)x[T_{ck}-\Delta T]
$$
上述两个式子表示了两个乘积,这两个乘积表述了中间样本点离左侧和右侧的样本点的距离远近关系。如果两个样本点之间的距离是恒定的,则两个乘积理应相同。如果将样本点的数量扩展到一定数目,则上述两个乘积则转变为乘积和的平均值,这个量实际上就是一定数量的样本点组成的一段有限长信号的自相关值,则这两个自相关值的差值可以表述为如下所示的式子。
$$
\overline{D_{\Delta t}}=R_x(T_{CK}-\Delta T)-R_x[-(T_{CK}+\Delta T)]
$$
根据自相关函数的特性,自相关函数是一个偶函数,根据偶函数的特性,上述方程可以转换为如下式子,
$$
\overline{D_{\Delta t}}=R_x(T_{CK}-\Delta T)-R_x(T_{CK}+\Delta T)
$$
如果$\Delta T$足够小,则上述方程可以写为如下式子,
$$
\overline{D_{\Delta T}}\approx-2\Delta T\frac{dR_x}{d\tau}|{\tau=T{CK}}
$$
由上述式子我们便可以获取中间样本点的偏离方向,偏离方向获知之后便可以进行校准了。
获知这个方向之后,我们可以通过设置校准补偿来进行调节,调节可变延时线直到自相关的差值为零为止。这种校准方法是模拟的方法,当然也可以使用数字的方法进行校准,数字方法校准认为在两个样本点之间的信号是一段直线,基于这个原理可以进行全数字的校准。

