昨天世界杯阿根廷夺冠了!
先写一个见证历史的时刻,阿根廷足球队在艰难的拼搏下获得了世界杯冠军的荣耀,整个过程真的是跌宕起伏,像是人生一样,经历了大起大落,感觉法国队和阿根廷队谁获得冠军真的需要依靠一些运气,你要说阿根廷队完全碾压法国队也没有,甚至比赛的最后时间在97s内姆巴佩连进两球之后以及在之后的加时赛中,阿根廷差点大门就要失守,还好马丁内斯扛住了考验,在之后的点球大战里,马丁内斯凭借出色的预判技巧以及运气,帮助阿根廷队获得了冠军,今夜属于阿根廷! ⚽ 🥇 🇦🇷
回到ADPLL,为什么写这篇文章?
写这篇文章的目的主要是帮助之后的自己快速理解一些概念,在之后有概念不清晰的时候还能再回来看看 😄。这篇文章主要是帮助我记忆和理解Robert Bogdan Staszewski的Phase-Domain All-Digital Phase-Locked Loop这篇文章,在这篇文章里,Bogdan主要介绍了ADPLL的基本相位域模型。
ADPLL的框图模型
ADPLL的基本模型如下图所示,
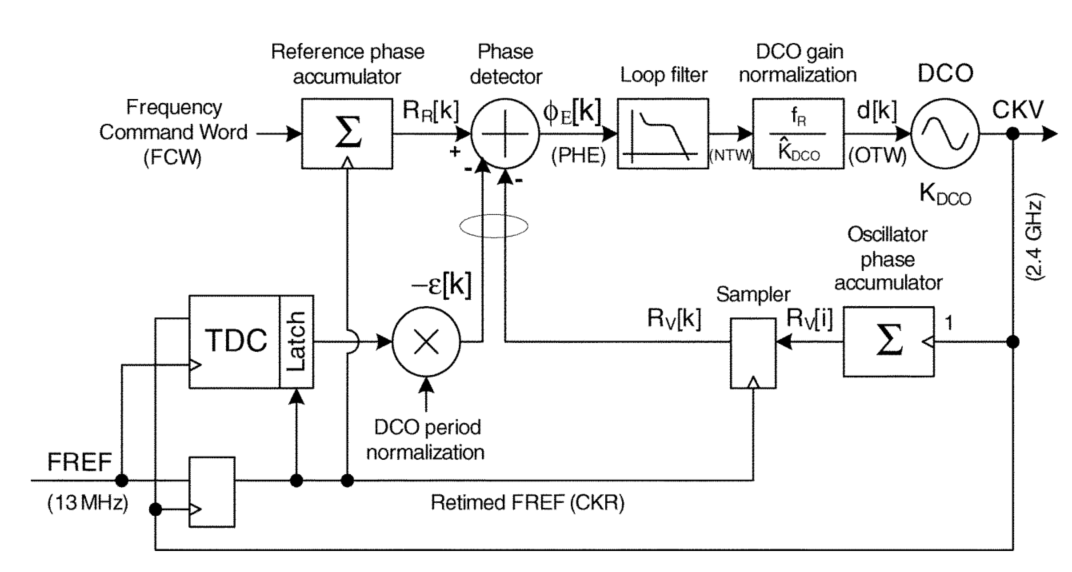
其基本原理就是通过两个计数器,计数器的计数触发信号分别为参考时钟和可变时钟,这里的可变时钟指的是频率综合器生成的目标时钟,比方说10GHz、1GHz这种比较高速的时钟;而参考时钟一般就是比较低速的了,例如,50MHz这种速率的时钟。这里给出了具体时钟的大小的目的不是说所有的ADPLL的参考时钟和可变时钟都是个速率,而是给读者一个概念,这两个时钟应该是差了好多数量级的。
计数器对参考时钟和可变时钟这两个时钟进行计数时,每一次时钟边沿累加的量是不一样的,
$$R_V[n]=\sum_{i=0}^{n}1$$
$$R_R[n]=\sum_{i=0}^{n}FCW$$
可以看到,参考时钟计数器使用的累加量是FCW,也就是频率控制字,而可变时钟计数器使用的累加两是1。如何理解呢?其实这里都是统计了在一定时间内可变时钟走过的边沿个数;一个假设CKV是CKR的频率的FCW倍,那么在一个CKR的时钟周期里,应该走了FCW个CKV的上升沿。这里就全部可以说得通了,Phase Detector中检测的就是两个信号在走过时,CKV应该有的上升沿、以及CKV实际走过的上升沿的差,再通过TDC实现再一个CKV周期内的相位差的检测,就可以得到当前时刻下,实际CKV走过的上升沿和CKV应该走过的上升沿的差了。
ADPLL时钟同步问题
CKR时钟被高速的CKV时钟clocked,这里说的被clocked的意思是被同步,我们说A时钟被B时钟clocked也就是说,A时钟同步到B时钟的边沿,换句话说,A时钟的边沿通过某种方式与B时钟的边沿在同一时刻发生,这样就保证了数字系统内时钟的同步性。
原先没有同步前的CKV与CKR的相位关系可以表达如下式
$$\theta_V[k]=k$$
$$\theta_R[k]=k\cdot N+\theta_0$$
其中,k表示第k个上升沿,$\theta_V[k]$表示了第k个CKV的上升沿的相位,当然,这个相位信息归一化为走过的CKV周期的个数;$\theta_R[k]$表示了到第k个CKR的上升沿时走过的CKV的周期个数。
同步之后的CKV与CKR变为如下所示
$$\theta_V[k]=k$$
$$\theta_R[k]=k\cdot N+\theta_0+\epsilon[k]$$
可以看到区别就在于在CKR的相位表达式中,多了一项$\epsilon[k]$,当然这一项表示了由于clocking或者说同步导致的相位损失或者增加,从这一含义中,我们可以知道$\epsilon[k]$的范围为$[0,1)$。
这一误差的存在会导致Phase Detector输出的数据不正常,因为Phase Detector回去的相位信息都是同步之后的相位信息,如下图所示,
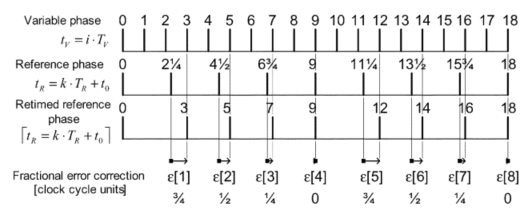
这是,如果我们使用同步之后的相位信息进行操作,我们会发现CKV与CKR之间会出现一个循环的误差,如果不考虑带宽限制,那么在输出上,就会体现出出现杂散Spurs的情况。这里的这个误差可以通过基于TDC的小数误差校正电路进行校正。
TDC校正电路
TDC的最小分辨精度和PLL的噪声是什么关系呢?
首先,我们要知道,TDC的噪声主要是量化噪声,假设TDC的量化精度为LSB,那么,量化时间噪声功率$\sigma_t^2$由下面的式子表达,
$$\sigma_t^2=\Delta t_{res}^2/12$$
根据上式,我们可以进一步转换,将$\sigma_t^2$转化为相位噪声功率$\sigma_\phi^2$,下面的式子的转换思路是将时间上的rms值与电压上的rms值通过斜率$A*\omega_v$做关联。
$$\sigma_\phi^2=\sigma_t^2(2\pi f_V)^2$$
那么将上面的两个式子做合并,我们就有下面的式子,
$$\sigma_\phi^2=\frac{4\pi^2}{12}\Delta t_{res}^2f_V^2 $$
由于量化噪声均匀分布在奈奎斯特带内,并且TDC的采样速率为参考频率的速率,所以我们可以有TDC导致的相位噪声谱密度为上式除以一个奈奎斯特频率$f_R$,如下式所示
$$\phi_{n,TDC}=\frac{4\pi^2}{12}\frac{\Delta t_{res}^2f_V^2}{f_R}[dBc/Hz]$$
为了有一个直观的感受,我们可以代入一些数字进去观察一下结果,例如,我们假设$f_V=2.4GHz$,$f_R=13MHz$,$\Delta t_{inv}=40ps$,计算结果如下表示
$$\phi_{n,TDC}=10log(\frac{4\pi^2}{12}\frac{(40ps)^2(2.4GHz)^2}{13MHz})=-86dBc/Hz$$
相位域信号的模运算
由于相位域的数据不可能无穷大,所以要限制给定相位域中的数据的带宽,带给定带宽下,如何去比对两个数据的大小?
其实,在数字电路里,采用有限带宽的数据直接就可以保证两个数据在做减法的时候,可以获取想要获取的小角度数据,例如下图所示,
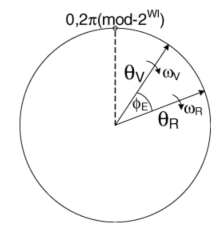
ADPLL的相位域模型
ADPLL的相位域模型如下图所示,
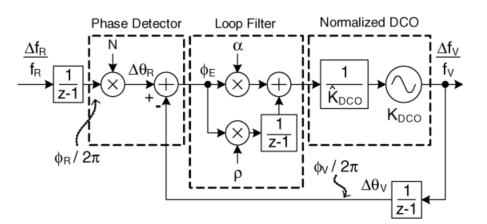
可以看到,该模型是一个线性模型,且用$z$域表达,为了我们可以更好地分析系统的稳定性等性质,我们需要将系统转换到连续域$s$域当中进行分析,这其中涉及到$z$域到$s$域的一个近似问题。
具体来说,$z$的定义如下所示,
$$z=e^\frac{s}{f_R}$$
其中,$s=j\omega=j2\pi f$,这里的$f$指的是信号变化的带宽,如果信号变化的带宽远远小于采样频率$f_R$,那么,我们可以得到下式的关系,
$$z=\lim_{s<<f_R}e^\frac{s}{f_R}\approx 1+\frac{s}{f_R}$$
其本质上就是一个等价无穷小。如果我们将上面的式子带入到模型中,我们可以获得下图所示的模型。
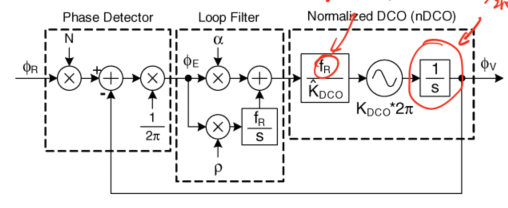
其中,对于累加器的近似由下式表达,
$$\frac{1}{z-1}\approx\frac{1}{1-1+\frac{s}{f_R}}=\frac{f_R}{s}$$
值得注意的是,这里的积分器有一个有限的增益为$f_R$,所以在后面会存在特殊的增益项$f_R$。
计算开环传输函数
实际上,电路的开环传输函数已经非常显然了😃,其中需要特别注意的是,在计算电路的开环传输函数的时候,我们不能把$N$这个增益项算在里面,因为反馈回路并没有把$N$包纳在里面。这里我们可以陈述一个结论,反馈系统的计算从反馈结束点开始到反馈开始点结束,这里的反馈结束点就是Phase Detector中的加法器,称为反馈结束点的原因是因为反馈回路在此点结束,汇入开环路径;这里的反馈开始点就是输出,称为反馈开始点的原因是因为反馈回路从输出位置开始和开环路径分离,开始形成了一个单独的回路。
那么,电路的开环传输函数由下式表示,
$$H_{ol}(s)=\frac{1}{2\pi}\cdot(\alpha+\frac{\rho f_R}{s})\cdot\frac{f_RK_{DCO}2\pi}{\hat{K}_{DCO}s}=\frac{\alpha f_Rs+\rho f_R^2}{s^2}$$
$$=\frac{\alpha f_Rs+\rho f_R^2}{s^2}$$
计算闭环传输函数&阻尼系数等参数
电路的反馈系数为1,我们可以马上写出电路由$\phi_R$到$\phi_V$的传输函数,如下所示,
$$\frac{\phi_V}{\phi_R}=N\frac{H_{ol}(s)}{1+H_{ol}(s)}=N\frac{\alpha f_Rs+\rho f_R^2}{s^2+\alpha f_Rs+\rho f_R^2}$$
可以看出该系统是一个两极点,一零点系统,根据自动控制原理,我们可以按照二阶系统的基本模型进行自然频率,阻尼系数等的设计。
$$\alpha f_R=2\zeta\omega_n$$
$$\rho f_R^2=\omega_n^2$$
由上述表达式可以解出自然频率$\omega_n$以及阻尼系数$\zeta$的表达式,并且可以看出,由于传输函数是二极点系统,所以这是一个Type II的PLL。
结语
那么,这篇文章到这里就结束了,本篇文章主要内容参考了一篇TCAS II文章:“Phase-Domain All-Digital Phase-Locked Loop”,由Bogdan写的,内容对设计非常有帮助,感兴趣的读者可以阅读一下。
在之后的文章里,我想写一写关于各种通信标准的来源以及推导的,比方说GSM通信、3G通信等。这将会帮助我们更好地理解PLL、ADC等器件的指标参数等。
那么这篇文章到这里就结束了✔,有问题的同学可以在评论区留言哦!😃

