ADPLL相位域MATLAB模型

写在前面✔

本文章主要的目的是为了给ADPLL的MATLAB模型做一个注释，并且解释编写代码过程中遇到的问题，以后我可能将代码上传到Github的私有仓库中，方便后期的使用。

整体思路

需要先在MATLAB中，根据Leeson Equation计算出需要的PLL带宽，其实Leeson公式说了那么玄幻的东西，根本上来说就是下面的式子，

$$
L(\Delta \omega)=\alpha\frac{\omega^2}{\Delta \omega^2}
$$

Leeson公式所表示的量的单位为$dBc/Hz$，所以从本质上来说，指的是功率谱密度，之所以有自变量的平方在分母上，一方面是因为VCO中存在$\frac{1}{s}$的项，另一方面，Leeson公式表示的量为功率了，给平方了。

通过Leeson公式可以根据GSM中的$-162dBc/Hz$的Reference值反推在特定信号频率$\omega$下，VCO或者说DCO的相位噪声估计表达式，进而根据给定的均方根抖动(Jitter RMS)得出PLL所需要的带宽。

在得到PLL的带宽之后，PLL的带内噪声也马上就可以知道了，直接从Leeson公式上获得即可。

给定ADPLL参数

此处给定了ADPLL设计需要的一些参数：

• fR：参考频率，设定为100MHz；
• fV：可变频率，设定为30GHz；
• FCW：频率控制字，本质上为$\frac{fV}{fR}$，这里为300；
• jitter_rms：抖动的均方根值，设定为50fs；
• PhaseMargin：环路的相位裕度，设定为60度（角度值）。

计算ADPLL的DCO相位噪声谱密度alpha_L_val

此处计算的方法是待定系数法，由于DCO器件的热噪声的功率谱密度由DCO积分后，由下式表达，

$$
L(\Delta\omega)=\frac{\alpha_L\omega_v^2}{\Delta\omega^2}=\frac{\alpha(\omega_v)}{\Delta\omega}
$$

这里有几点需要注意的，首先是$\alpha(\omega_v)$是可变频率函数，对应不同频率处的相位噪声谱密度是不一样的，所以这一点需要提前考虑在内，否则会导致最后的数据出错；另一个问题是这个函数要确定到底采用角频率还是使用Hz作为频率的单位，因为在之后做积分进行带宽计算的过程中，不同的单位会导致结果相差一个$2\pi$，具体来说，可以用下面的式子进行说明，

$$
\int^\infty_{BW}L(\Delta\omega)d\Delta\omega=\int^\infty_{BW*2\pi}\frac{\alpha_L\omega_V^2}{\Delta\omega^2}d\Delta\omega=2\pi\int^\infty_{BW}\frac{\alpha_L f_V^2}{\Delta f^2}d\Delta f
$$

所以，我们需要在这里仔细规定频率到底是以角频率为单位进行计算，还是以Hz为单位进行计算的，在整体的程序中，要保持一致，以防止出现错误。

计算ADPLL的带宽

这里采用待定系数法，先待定出$\alpha_L$的大小，再进一步代入我们想要的中心频率大小，就可以得到一个以频偏$\Delta\omega$为自变量的噪声功率谱密度的函数$L(\Delta\omega)$了。为了得到其与抖动$jitter$的关系，我们可以使用下面的关系，

$$
jitter_{rms}2\pi f_V=\sqrt{\int^\infty_{BW}\frac{\alpha_L f_V^2}{\Delta f^2}d\Delta f}
$$

上面的关系的本质是，抖动与相位噪声功率的rms值是通过斜率$2\pi f_V$联系起来的，这一点再ADI的一篇博客中有做解释，这里就不再进行解释了，本质上就是一个求导的过程。

另外，此处进行计算使用的$jitter_{rms}$的大小为$50fs$，带内$25fs$（TDC量化噪声）与带外$25fs$（DCO热噪声）均匀分配，得到最终的结果。这里需要注意的是，这里考虑的还不够完善，因为根据这种计算的出的TDC量化噪声不仅仅再带内有$25fs$的jitter贡献，还有带外$25fs$的jitter贡献。

其实，读者仔细思考一下，这里的带内&带外$25fs$的抖动总和为$50fs$的描述本身就是有问题的，因为抖动本身就是标准差，对于标准差而言，两个$25fs$标准差的和为$25\sqrt{2}fs$，所以我们实际应该设计的抖动大小为$25\sqrt{2}\approx35fs$。

最终程序计算出来的ADPLL的带宽应该在$611kHz$处。

计算ADPLL的环路参数

在计算ADPLL的环路参数的时候，需要考虑闭环传输函数对噪声的影响，目前我还没有对这个进行考虑。整个环路的图如下图所示，

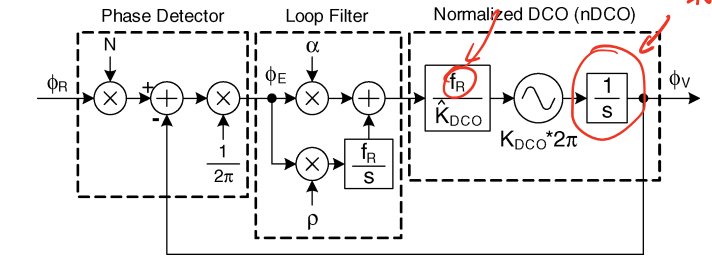
可以看到的是，本系统的滤波器为一阶滤波器，其传输函数如下所示，

$$
TF_{filter}=\alpha+\frac{\rho f_R}{s}
$$

可以看到这个滤波器贡献了一个@origin的极点；贡献了一个位于$\frac{\rho f_R}{\alpha}$的零点。

DCO的传输函数如下所示，

$$
TF_{DCO}=\frac{f_R2\pi}{s}
$$

可以看到DCO贡献了一个@origin的极点。

电路的总开环增益为，

$$
OLTF = \frac{f_R}{s}(\alpha+\frac{\rho f_R}{s})
$$

接下去需要根据两个条件解出$\alpha$和$\rho$的值，两个条件分别是

1. BW处增益为$0dB$
2. BW处相位为$60$

由于BW的值在先前的模块中已经求解出来了，为$611kHz$，所以两个条件一定可以解出两个未知数，如下式所示

$$
\begin{cases}
(\alpha f_RBW2\pi)^2+\rho^2f_R^4=(BW2\pi)^4 \
\frac{\alpha BW2\pi}{\rho f_R}=tan(\frac{PM\pi}{180})
\end{cases}
$$

代入参数之后可得$\alpha=3.32\times10^{-2}$，$\rho=7.3659\times10^{-4}$

计算TDC的量化噪声水平以及精度

此处的TDC量化噪声是根据带宽处的DCO热噪声引起的相位噪声曲线的插值给出的，用数学表达式如下所示，注意此处为单边谱，并且相位噪声自变量的单位为Hz。

$$
S_{N,TDC}=L(BW)
$$

这里通过计算可以得知$S_{N,TDC}=-101.3947dB$，注意这里是单边谱的功率谱密度。

接下去我们希望计算一下TDC需要的绝对精度大小，这里我们就需要推导一下TDC的量化噪声。量化噪声功率一般由下式表达，

$$
NoisePower_{Q}=\frac{LSB^2}{12}
$$

在TDC中，LSB就是我们的时间精度，我们可以指定时间精度为变量$t_{res}$，代入上述公式可以知道我们TDC的”噪声”功率大小，如下所示，

$$
NoisePower_{TDC}=\frac{t_{res}^2}{12}
$$

这个地方需要说明的是，这里的”功率”没有实际的意义，只是一个统计上方差的概念，现在我们把方差变为标准差，

$$
\sigma_{TDC}=\frac{t_{res}}{\sqrt{12}}
$$

接下去使用抖动rms（标准差）和相位噪声rms的关系有，

$$
\sigma_\phi=2\pi f_V\sigma_{TDC}=\frac{2\pi f_V t_{res}}{\sqrt{12}}
$$

量化噪声总功率均匀分布在奈奎斯特带内，即$[-\frac{f_s}{2},\frac{f_s}{2}]$之间，所以单边谱密度可以用如下表达式，

$$
L=\frac{\sigma_\phi^2}{f_s/2}=\frac{(2\pi f_Vt_{res})^2}{6f_s}
$$

所以可以反向导出$t_{res}$关于L（单边谱密度）的函数，如下所示

$$
t_{res}=\frac{\sqrt{6f_sL}}{2\pi f_V}
$$

通过计算可知，$t_{res}=1.108ps$

此外，读者还需要关注TDC量化噪声到输出的传输函数，因为TDC量化噪声作用在鉴相器的位置，所以可以认为是输入，其传输函数就是整体的闭环传输函数，如下所示，

$$
CLTF=\frac{OLTF}{1+OLTF}=\frac{\alpha f_Rs+\rho f_R^2}{s^2+\alpha f_Rs+\rho f_R^2}
$$

在相位裕度为$PM=60$时，其BODE图如下所示，

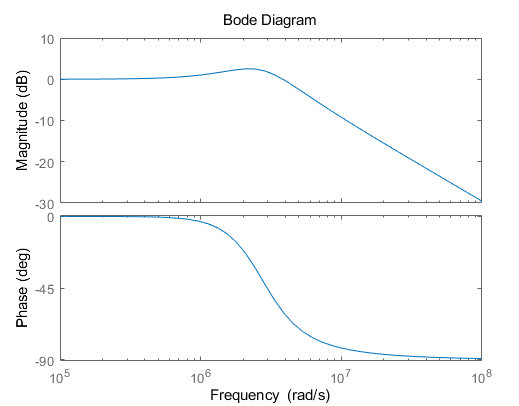
可以看到在带宽处有3dB左右的突起，这部分有可能会影响到最后的积分大小，需要仔细考虑，这一部分我还没有进行考虑，不过就目前的结果来看，对于jitter的影响不大，如果就这个理想的传输函数来说，也就增加了$3fs$的均方根抖动。

最终的噪声谱密度如下图所示，

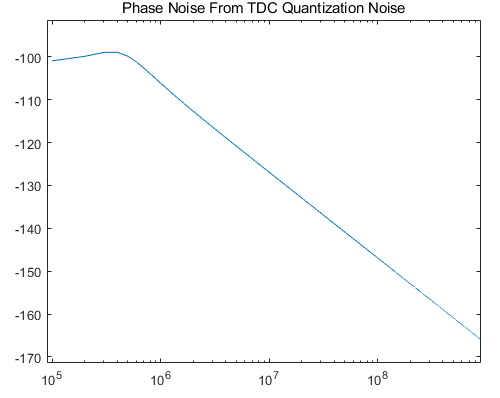
可以看到TDC的量化噪声谱密度在带内表现为平带噪声，但是在带外会以$20dB/dec$的速度进行滚降，这个速度太过缓慢，会导致带外的TDC噪声不能被有效抑制，这部分噪声与DCO的热噪声相当了，肯定是不行的。解决的办法可以是采用高阶环路滤波器实现，目前使用的环路滤波器还是一阶的，可以采用二阶的环路滤波器实现。

计算DCO量化噪声

DCO的量化噪声功率也可以使用TDC一样的量化噪声功率进行计算，如下所示，

$$
\sigma_{DCO}^2=\frac{f_{res}^2}{12}
$$

这一部分量化噪声的功率其实是均匀分布在奈奎斯特带内，即$[-\frac{f_s}{2},\frac{f_s}{2}]$之间，所以单边谱密度可以由下式表示，

$$
L=\frac{\sigma_{DCO}^2}{f_s/2}=\frac{f_{res}^2}{6f_s}
$$

要注意DCO量化噪声作用的位置我还没有非常明确，我目前是加在振荡器前，但是加在normalization之后，这样做的原因还是不是非常明确。

以上述位置施加量化噪声之后，我们需要知道传输函数的表达式，该位置到输出的开环传输函数为，

$$
OLTF_{DCO}=\frac{2\pi}{s}
$$

其闭环传输函数就是在上式的基础之上加上一个如下的系数即可，

$$
CLTF_{DCO}=\frac{OLTF_{DCO}}{1+OLTF}=\frac{s^2}{s^2+\alpha f_Rs+\rho f_R^2}\frac{2\pi}{s}=\frac{2\pi s}{s^2+\alpha f_Rs+\rho f_R^2}
$$

我们可以分析一下这个闭环传输函数的系数，当频率达到环路带宽之后，基本上就不会对噪声产生影响了，唯一有影响的就是开环的增益，也就是$20dB/dec$的滚降；然而在带内，我们可以看到，噪声会以$20dB/dec$速度滚升，这是由于@origin的零点造成的。

其实带内的对于噪声的抑制也不够，根据之后的仿真结果，带内的DCO量化噪声会额外产生$30fs$的rms抖动，造成总的rms抖动从$36fs$上升到$47fs$。所以呢，可以考虑采用一些其他的计数来抑制带内的DCO量化噪声，可以考虑DSM，使用抖动将低频量化噪声功率抖到高频去，再通过环路滤波器滤除这一部分噪声功率。注意：以上分析都是按照我自己的理解分析的，合理性还需要进一步考证。

将计算出来的参数代入Simulink模型中进行分析

本程序的特色在于可以可视化地进行建模，即使用Simulink进行可视化的相位域建模。Simulink模型的主框图如下所示，

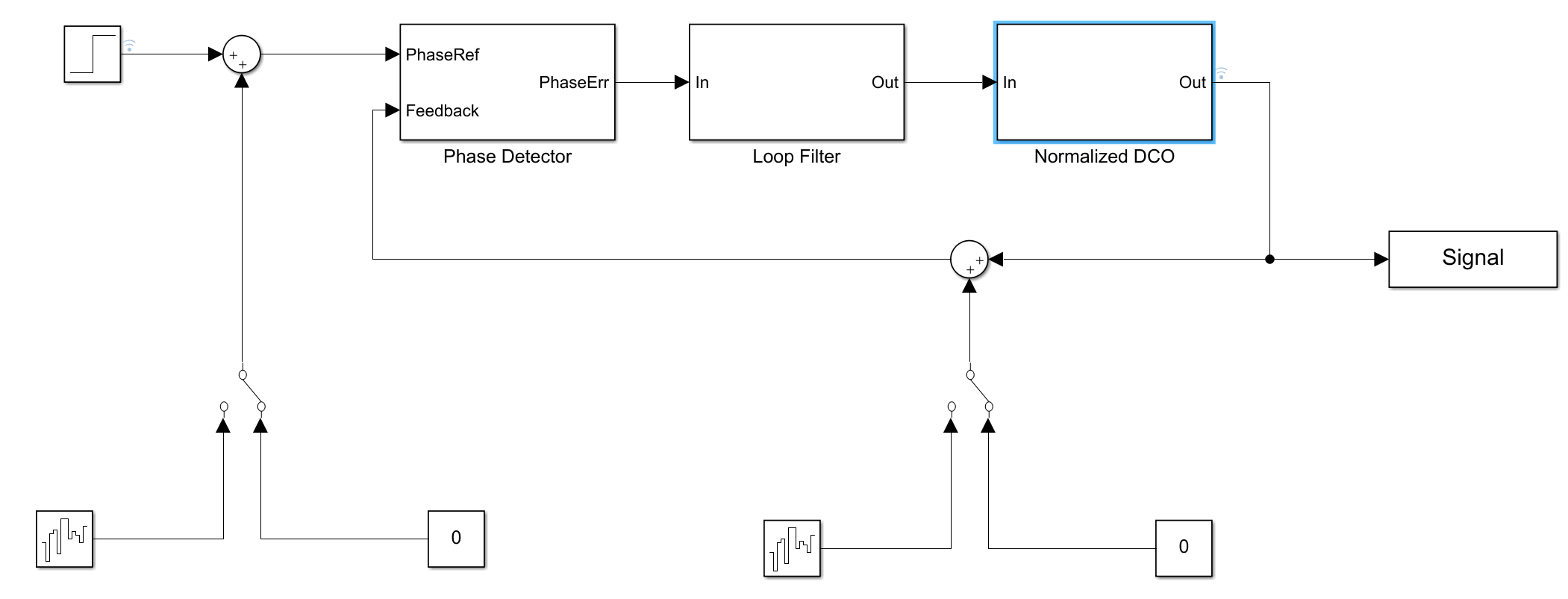
这一部分模型可以看到不是特别复杂，主要包括了鉴相器、环路滤波器和DCO，噪声是通过Band-Limited White Noise的模块产生的，最后的输出由To Workspace模块抓取并以数组形式返回到Matlab工作区，基本的模型就是这样的，下面我们来仔细看看这些模块建模的时候是怎么考虑的，并且有哪些需要注意的。

首先一个要注意的是，本模型是相位域模型，理论上，一个sinWave的信号的相位是不断增长的，但是这里却采用了阶跃信号作为相位域模型的输入激励，有同学可能就要问了，为什么这里不是采用ramp信号呢？并且最后采集的Signal理论上也是一个阶跃信号，你怎么能够分析出相位噪声这种信息呢？

其实在一开始建模的时候，本人采取的策略是再输入使用阶跃信号模拟频率的变化，然后利用一个积分器产生对应的相位信息，再用这个相位信息作为模型的输入，输出的相位信息通过一个sin模块之后产生对应的sinWave，再将sinWave做fft之后采取其主频的边带放大后作为PhaseNoise的功率谱密度。当然，这是可行的，但代价是非常长的仿真时间，以及巨大的计算量。

读者可以想象，对一个$30GHz$的信号的相位，这个相位信息的数据规模会随着时间的增长而增长，并且由于Signal需要识别到$30GHz$的正弦波，频谱的范围就要扩展到至少60GHz，假设$100GHz$的采样率，对于时域来说，时间分辨率就要为$10ps$，并且频谱的分辨率至少为$10KHz$，因为我们需要足够低频的分量才能看清带内噪声，在这个前提下，时域数据的时间长度要至少为$100\mu s$，这个的数据量消耗是非常巨大的，并且会导致仿真时间到一个无法接受的长度。

在这个背景下，这个模型采用了一种技巧，避免了采样$30GHz$信号的操作，而是直接对一个DC量进行采样，这一部分其实可以进行数学层面的推导，在这里，我仔细推导一下。

在推导之前，先要熟悉一下我们之前高数学过的欧拉公式(Euler’s Formula)，如下所示，

$$
e^{j\omega t}=cos(\omega t)+jsin(\omega t)
$$

欧拉公式的复$e$指数函数的傅里叶变换对应的就是$\delta$函数，所以可以认为我们傅里叶变换里的building block在频域上是$\delta$函数而在时域上就是我们的复$e$指数，如下

$$
e^{j\omega_0 t}=2\pi\delta(\omega-\omega_0)
$$

在图形上可以认为是右半边频谱的一根单独的谱线，我们可以想象，左侧时域中的相位为$\omega_0t$，所以一种常用的方法就是想象我们的频谱是一个三维坐标，三个维度的信息分别是$\omega$频率、$Re$实数轴、$Im$复数轴，实数轴与复数轴共同决定了我们的相位信息（$arctan\frac{Im}{Re}$）以及幅度信息（$\sqrt{Im^2+Re^2}$）。

所以我们可以使用Phasor Diagram（三维坐标）来理解我们的信号。我们只需要记住一个结论，就是$sin$函数比$cos$函数要滞后$90$，体现在频谱上就是sin的起始Phasor向量是$1\angle0$，而cos的起始Phasor向量是$1\angle-90$。这样我们又多了一种全新的方法来理解我们的欧拉公式，想要获得位于右半轴的$e^{j\omega t}$的频谱，我们只需要将$sin$函数提前$90$即可，在复数域中，表示这一操作只需要乘以$1\angle 90 =j$即可，可以看到和我们的欧拉公式是完全符合的。

$$
e^{j\omega t}=cos(\omega t)+jsin(\omega t)
$$

假如我们现在在有用信号上叠加了一个$\phi(t)$，如下所示

$$
Signal=sin(2\pi f_Vt+\phi(t))
$$

利用和差化积公式，可以进行分解，得到下面的表达式，

$$
Signal=sin(2\pi f_Vt)cos(\phi(t))+cos(2\pi f_Vt)sin(\phi(t))
$$

如果我们的$\phi(t)$足够小，在我们的这个情况中是符合的，因为

$$
3\sigma_\phi=2\pi f_Vjitter_{rms}=3\cdot2\pi(30\times10^9)(50\times10^{-15})\approx9.42\times10^{-3}\times3\approx\frac{9\pi}{1000}\rightarrow1.62
$$

上述式子表明$99.7%$的jitter变化都会在$1.62$以内，我们再来分析一下这个误差大概是多少，

$$
sin(\frac{9\pi}{1000})-\frac{9\pi}{1000}=-3.7671\times 10^{-6}
cos(\frac{9\pi}{1000})-1=-3.9969\times 10^{-4}
$$

假如上述的误差在应用中可以接受，那么可以转换为下面的表达式

$$
Signal=sin(\omega_0 t)+cos(\omega_0 t)\phi(t)
$$

上面的这个式子告诉我们，因为加上$sin(\omega_0 t)$在频域中相当于对中心频率进行操作，并不会产生其他的频率分量，这是由我们的时域和频域的线性性质保证的；另一方面，乘上$\phi(t)$在频域中相当于对中心频率和$\phi(t)$做了混频（卷积）操作，对我们希望了解的边带信息进行了一个频谱的搬移$\delta(\omega-\omega_0)*\Phi(\omega)$，也就是使用$\omega_0=0$还是$\omega_0=30GHz$，最终获得的边带信息是一样的。所以我们从理论上证明了，相位域模型在DC处工作的相位噪声谱密度和在30GHz处工作的相位噪声谱密度是等价的。

所以我们采用的方案是使用一个阶跃信号来作为激励验证环路的相位裕度等信息，并截取环路settle之后的时域输出信号进行频谱分析，获取我们的相位噪声。

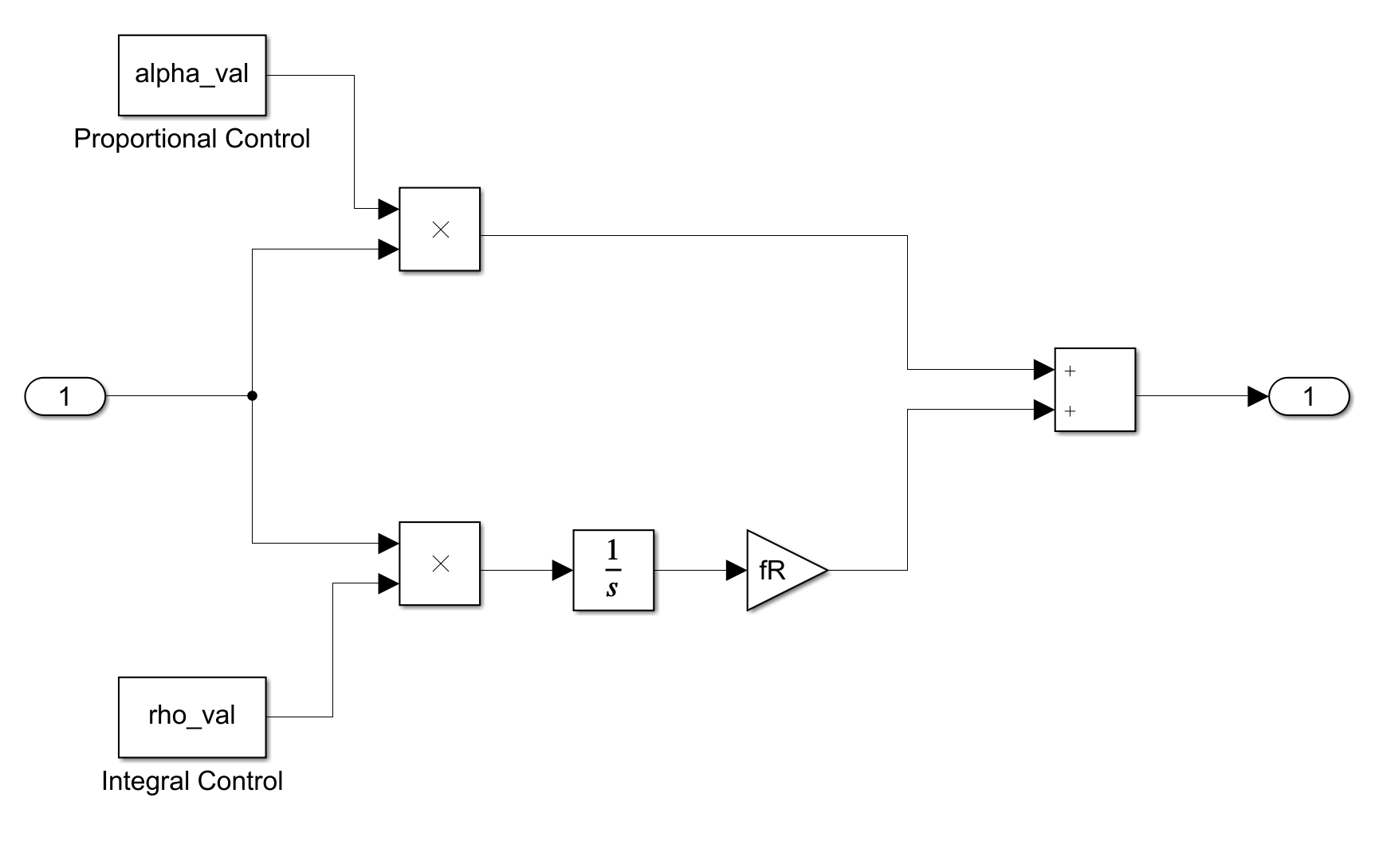
接下来介绍Phase Detector模块，其内部还没有考虑TDC的增益，仅仅是对相位信息做了个加法，并且除以$2\pi$将相位信息由弧度的单位转换为fV时钟周期的个数。

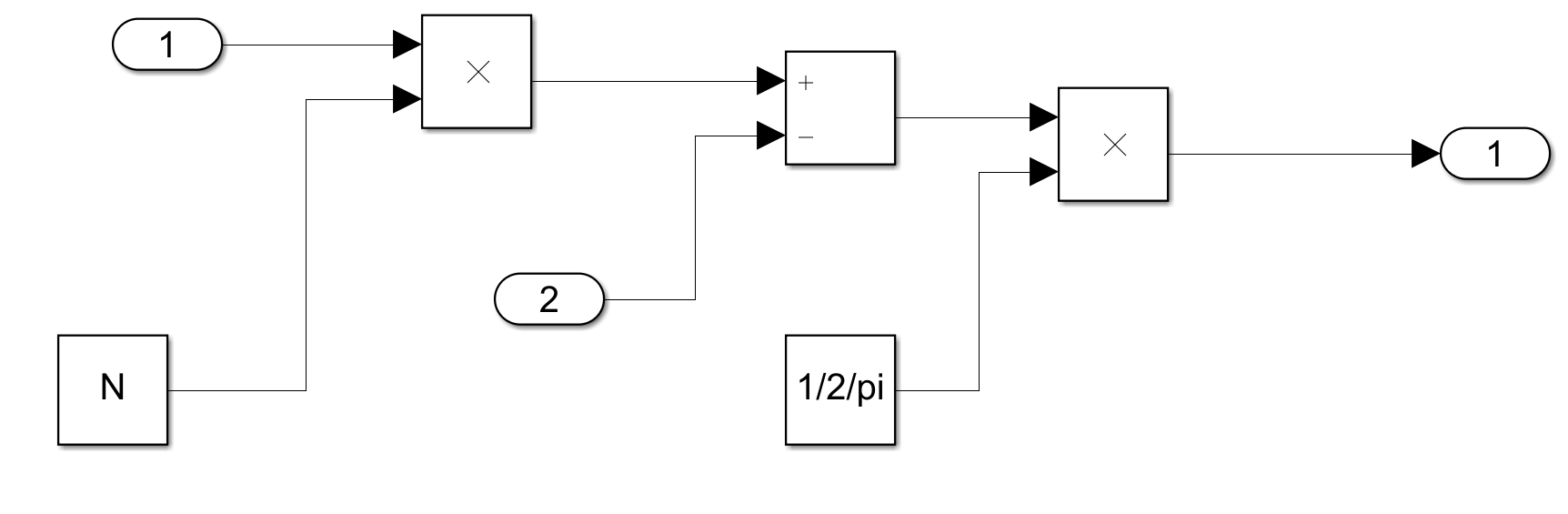
接下来介绍Loop Filter，目前的Loop Filter实际采用的是一阶IIR滤波器，转换为s域波形后，如下图所示，

该一阶滤波器存在的问题就是对TDC的带外噪声抑制只有$20dB/dec$，目前从仿真的角度来看是不能满足我们的需求的，后期可能会通过提升滤波器阶数的形式来提升系统对TDC带外噪声的抑制能力。

接下来介绍我们的DCO模型，DCO模型的量化噪声是通过Band-Limited White Noise给定的，并且其中的fR倍数来自于$z$域到$s$域的转换，$2\pi$的作用是之前提到的单位转换，并且DCO内部本身的积分器由$\frac{1}{s}$模块进行建模。

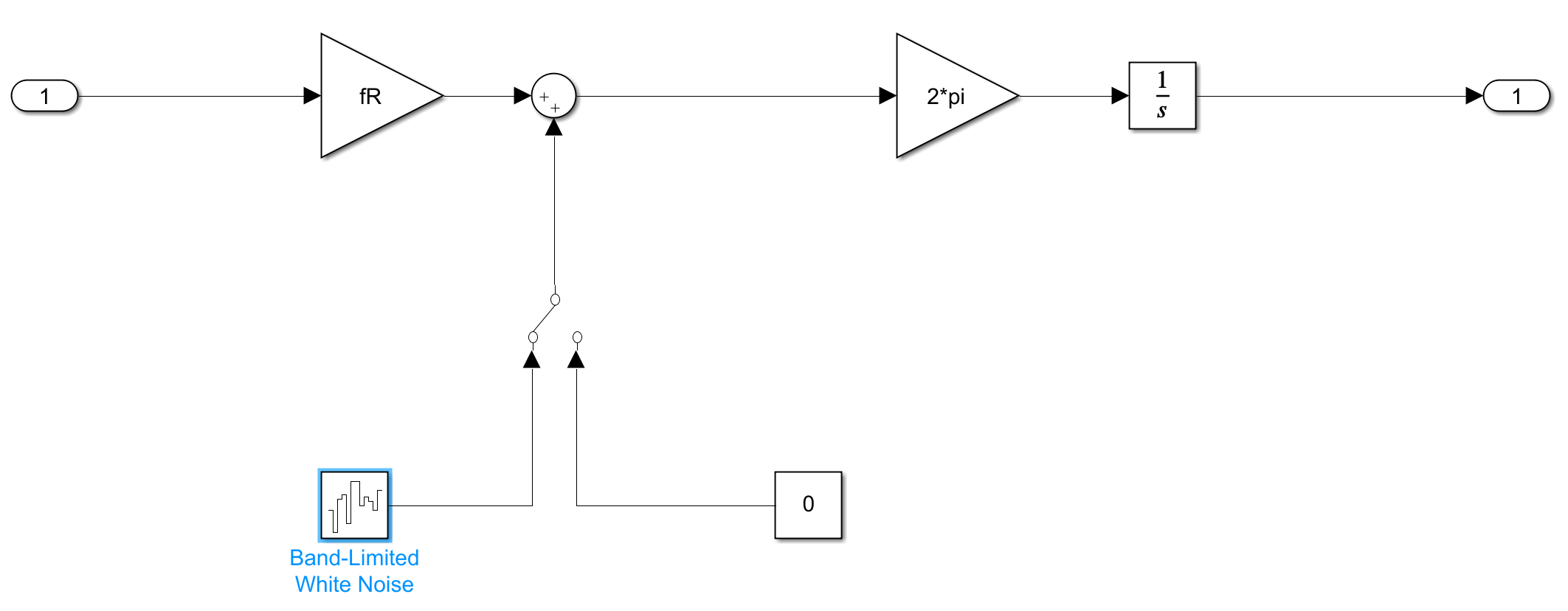
获取Signal数据并做傅里叶变换生成我们的相位噪声谱密度，并计算RMS抖动

这一部分功能主要是通过FFTspectrum的函数实现的，其代码如下

function [SpectrumSSB] = FFTSpectrum(Signal,Fs)
    Signal_window = length(Signal)*1/Fs;
    Spectrum_Resolution = 1/Signal_window;
    Spectrum_Complex = fft(Signal);
    Spectrum_Magnitude_DSB = abs(Spectrum_Complex)/length(Signal);
    for i=2:length(Signal)/2
        % Pay Attention to sqrt(2). This is required due to magnitude
        % spectrum being added is equivalent to multiplied by sqrt(2)
        Spectrum_Magnitude_SSB(i) =  (Spectrum_Magnitude_DSB(i+1)+Spectrum_Magnitude_DSB(length(Signal)+1-i))/sqrt(2);
    end
    Spectrum_Magnitude_SSB(1) = Spectrum_Magnitude_DSB(1);
    L = 10*log10(Spectrum_Magnitude_SSB.^2/Spectrum_Resolution);
    semilogx((0:Spectrum_Resolution:length(Signal)/2*Spectrum_Resolution-Spectrum_Resolution),L);
    title('Phase Noise');
    xlabel('Hz');
    ylabel('dBc/Hz');
    SpectrumSSB = Spectrum_Magnitude_SSB;
end

可以看到的是，代码里fft的功能是使用matlab自带的函数实现的，这个产生了一个双边的复数谱，我们只对幅度和功率感兴趣，所以使用abs做了转换，产生了双边幅度谱，之后使用一个循环遍历我们的双边谱数列，将数据进行镜像翻转并叠加，产生我们的单边幅度谱，这里需要特别注意 ❗，我在这里犯了错误，花费了几个星期才找到，在幅度谱做叠加的时候，我们始终要记得频谱是功率叠加，所以幅度谱相加之后，要除以$\sqrt(2)$。之后我们也要注意在转换功率谱的时候直接做平方即可，但是在产生功率谱密度的时候，要除以频率分辨率的带宽，这是因为在做fft时，算法将频率分辨率内所有的功率叠加用一根谱线表示，这时候如果要知道密度，需要除以这一段的带宽，也就是我们的频谱分辨率，之后再进行对数显示即可。

在计算RMSjitter的时候，我们需要使用我们的功率谱，这里的设计时FFTspectrum函数将幅度谱作为参数传递出去，在函数外进行RMSjitter的计算，所以我们还需要做平方的操作才能转换为功率谱，这里由于计算总功率，直接将所有的谱线的功率进行叠加即可，最后使用下面的数学关系导出RMSjitter即可，要注意的是我们使用的全部都是单边谱，这一点不要搞错。

$$
jitter_{rms}=\sqrt{\frac{\sigma^2_{L}}{(2\pi f_V)^2}}
$$

最终结果

我们做了DCO量化噪声的仿真，确定了DCO量化噪声对输出相位噪声的影响，下图为DCO量化噪声产生的相位噪声的单边功率谱密度，蓝线为实际噪声源的结果，红线为理想噪声源的结果。

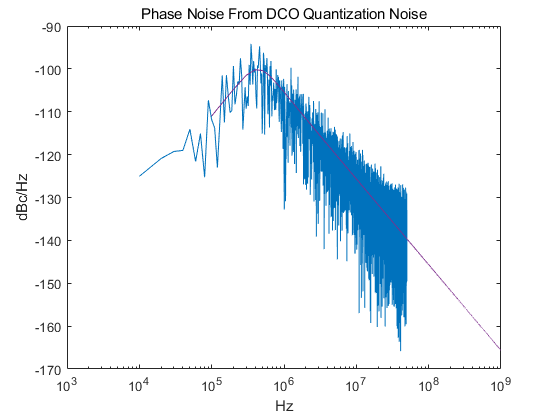
该频谱积分获得的RMSjitter和设计的jitter如下表格所示，

Nominal Jitter RMS	Output Jitter RMS
$36fs$	$33.6fs$

可以看到结果还是符合得很好的，注意，此时的DCO带内噪声根据评估后发现为$30fs$左右，总的$Jitter_{rms}$为$44fs$左右，意味着带内的噪声水平也不可忽略，可能考虑通过DSM实现将低频噪声抖到高频去。此外，还有一个值得思考的事情是，DCO的量化噪声我故意设置的和TDC的量化噪声以及DCO的热噪声相当，这时的频率精度为$127.59KHz$，可以看到，如果我们想要进一步压低我们的DCO带外量化噪声，使得DCO带外量化噪声的$Jitter_{rms}$的功率比DCO的热噪声的功率小一个数量级的化，根据我们的精度和噪声功率的公式，

$$
\sigma_{DCO}^2=\frac{f_{res}^2}{12}
$$

我们可以发现精度至少要提升$\sqrt{10}\approx3$倍左右，也就是说精度要提升到$40KHz$这个量级。这个数量级对于我们后期的设计来说也是具有指导性意义的。

我们还做了TDC量化噪声的仿真，先使用之前的程序计算出需要的TDC的量化噪声功率谱密度水平，再代入我们的Band limited White Noise模块中，就可以得到最终的单边谱密度了，如下所示，蓝线为实际噪声源的结果，黄线为理想噪声源的结果。

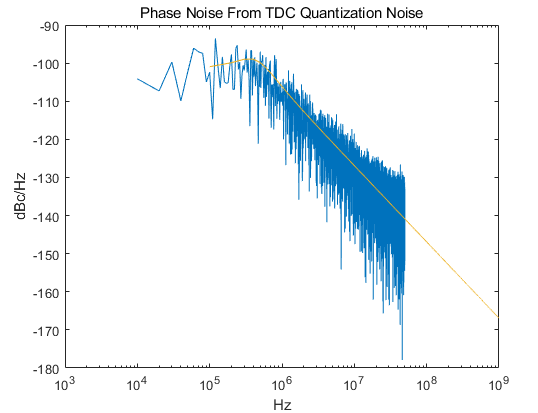
该频谱积分获得的RMSjitter和设计的jitter大小如下表格所示，

Nominal Jitter RMS	Output Jitter RMS
$50fs$	$50.454fs$

可以看到模型和理论计算符合得还是很好的，值得注意的是，在带外部分得TDC得量化噪声与我们的DCO的热噪声水平相当了，这是我们不希望看到的，我们希望至少带外要由DCO的热噪声和量化噪声主导，所以我们这里可能需要采用高阶IIR环路滤波器才可以满足我们的需求，否则我们就需要进一步提升我们的TDC的精度，这对于我们来说是比较困难的，所以后面可以采取2阶环路滤波器的设计，来降低我们的带外TDC噪声。

Miscellaneous

本代码运行在i7-7700HQ的2.8GHz的CPU的电脑，该电脑拥有16GB内存，代码存储在SSD上，运行时间经过测量为81.44s，大约为1min20s，可以看到这个代码的时间复杂度和空间复杂度都不高，完全可以在一般的个人PC机上运行，不需要额外的算力支持。