写在前面
本文的内容来自于
“Un-Ku Moon, K. Mayaram and J. T. Stonick, “Spectral analysis of time-domain phase jitter measurements,” in IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, vol. 49, no. 5, pp. 321-327, May 2002, doi: 10.1109/TCSII.2002.802343.”
我阅读这篇文章的主要目的在于弄清楚各种抖动的定义到底是什么,它们之间到底有什么关系。
jitter的种类
作者说通常用来描述jitter的量有,”period jitter”、”edge-to-edge jitter”、”cycle-to-cycle jitter”、”absolute jitter”、”tracking jitter”等等。
本文的目的就是总结这些量,并且弄清它们之间的关系。
抖动&相位噪声
假设一个理想的无抖动的信号为$s(t)$,带有抖动的信号为$s_j(t)=s(t+j(t))$,我们直接对上述两个信号做傅里叶展开,理想的信号如下,
$$
s(t)=c_1cos(\omega_ot)+c_2cos(2\omega_ot)+c_3cos(3\omega_ot)+···
$$
带有抖动的信号如下,
$$
s_j(t)=c_1cos(\omega_ot+\omega_oj(t))+c_2cos(2\omega_ot+2\omega_oj(t))+···\
=c_1cos(\omega_ot+\phi(t))+c_2cos(2\omega_ot+2\phi(t))+···\
$$
在有抖动的信号的傅里叶展开式里,有两种抖动的表达形式,一个是$\omega_oj(t)=\phi(t)$,我们马上可以看到这里有单位的转换了,$j(t)$的单位为$[s]$,$\phi(t)$的单位为$[rad]$。
我们把单位为$[s]$的$j(t)$称为时间抖动,Jitter;把单位为$[rad]$的$\phi(t)$称为相位噪声,Phase Noise。
所以这里我们搞清楚了相位噪声和抖动的关联与区别。
$rad^2/Hz$还是$dBc/Hz$
这里我在看Bogdan的文章”Event-Driven Simulation and Modeling of Phase Noise of an RF Oscillator”也存在疑问,他原文是这样描述的,
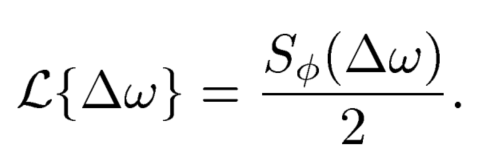
这里的谱的单位为$[rad^2/s]$,可是我一直以为是$[dBc/Hz]$,这两个到底有什么关联呢?作者马上给出了答案。
Narrow-Band FM Approximation
这里使用到了其实在”ADPLL相位域MATLAB模型”中我就推导过的一个近似方法。说起来也是挺有趣的,当时在做ADPLL的相位域模型,在测量输出信号的相位噪声的时候,我直接对几十GHz的信号做了采样操作,并且想要得到频谱分辨率为10kHz级别的相位噪声谱密度。(真是一个天真的想法)
上述操作是不行的,闫老师当时就指出了问题,我一直没有找到对应的理论,后来我在2023年初的春节假期里进行了推导,发现确实是那么回事,没想到推导的结论就是我们的窄带FM近似… 😄
这里就不做推导了,需要的话可以去我那篇文章里看看,这里就把结论直接写出来,
$$
a(t)=cos(\omega_ot+\phi(t))\approx cos(\omega_ot)-sin(\omega_ot)\phi(t)
$$
上述式子成立的条件就是$\phi(t)\rightarrow0$或者是$\phi(t)<<2\pi$。
如果是符合窄带FM特征的抖动,就可以直接将相位抖动$\phi(t)$的频谱放在基频$\omega_o$处。当然这样做需要换一下单位,由原先的[dBc/Hz]换成[rad^2/Hz]。
可以看到,这两个单位如果符合窄带FM近似的条件的话,是可以自由转换的,当然前提是必须要满足窄带FM近似的条件。
作者在这里还非常严谨地补充了,如果抖动不符合窄带FM近似地条件,那么相位噪声谱密度的形状是怎么样的,是一型Bessel函数的形状,我上网搜了一下,大概长下面这个样子,
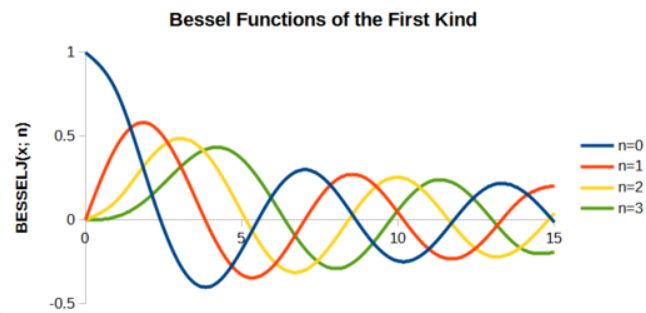
真的非常的诡异,作者为了防止我们进一步掉入钻研Bessel函数的陷阱,告诉了我们,”In the analysis of oscillator/PLL systems and applications, the narrow-band assumption is typically accurate”,也就是说在振荡器和PLL系统里面,一般窄带FM近似就足够准确了。
Two Most Commonly Used Jitter Types
作者说这里采用的描述和拉扎维的一篇论文”A study of oscillator jitter due to supply and substrate noise”比较类似,作者简单介绍了两种Jitter的类型,Period Jitter以及Absolute Jitter
Period Jitter
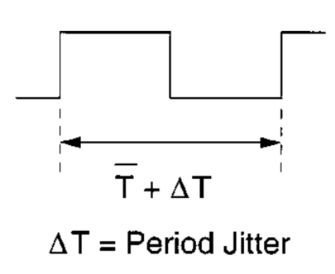
实际测量的变化是周期长度的变化,周期的定义为一个上升沿到下一个上升沿。因为测量的周期的变化,有些人称这种Jitter为edge-to-edge jitter、cycle jitter、cycle-to-cycle jitter。作者在这边还贴心地提示了,cycle-to-cycle jitter这一说法是有歧义地,如下所示,

作者说这种period jitter的描述一般在数字应用(例如微处理器)中经常采用,因为数字电路中比较关心时钟边沿之间的数据锁存情况。
Absolute Jitter
Absolute jitter,绝对抖动也是常用的一种抖动衡量办法,有的时候tracking jitter是这种抖动的另一个名字。作者说相对于tracking jitter,absolute jitter这个名字更加有用,所以作者采用absolute jitter来指代这种与理想源之间的绝对时间偏差。
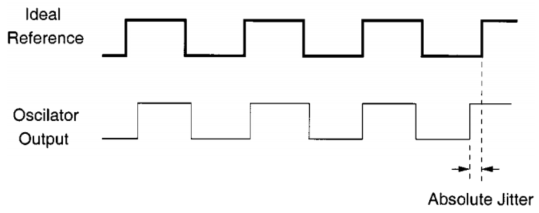
其他的名字
| 文章作者 | period jitter的别名 | absolute jitter的别名 |
|---|---|---|
| Maneatis | cycle-to-cycle jitter | tracking jitter |
| Herzel & Razavi | cycle jitter | long term jitter |
本文在使用名称的同时还会给出具体的表达式,以防止出现误解。
以二阶PLL为例讲解这些不同的jitter之间的区别
作者给出了二阶PLL相关的公式,并介绍了二阶PLL相关的概念,这些概念将会帮助读者进一步理解jitter之间的关联和区别。
测量开环PLL(单独工作的振荡器)
作者先给出了绝对抖动的定义,absolute jitter,如下图所示,
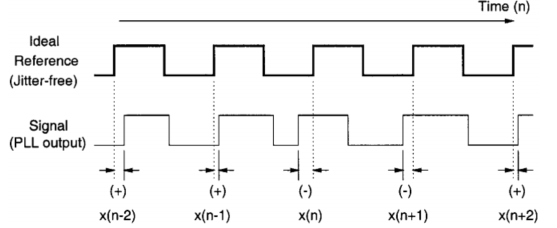
并且给出了一般的振荡器的相位噪声模型,$|X(\omega)^2|\propto1/\omega^2$,这是在只考虑白噪声的前提下的。
接着作者给出了周期偏移的定义:$p_1(n)=x(n)-x(n-1)$,假如两次时间戳偏移的大小和方向完全一样,那么周期偏移完全为零。接下去,作者又做了推广,如下,
$$
p_N(n)=x(n)-x(n-N)
$$
对于$\sigma_N^2$的大小,作者专门做了推导,过程比较复杂,最终的结果如下所示,
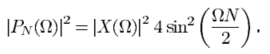
读者可以看到,随着$N$不断增大,起到的滤波作用就越小,当$N=1$时,低通滤波的效果是最强的,作者还绘制了图片来描述这一问题,如下所示,
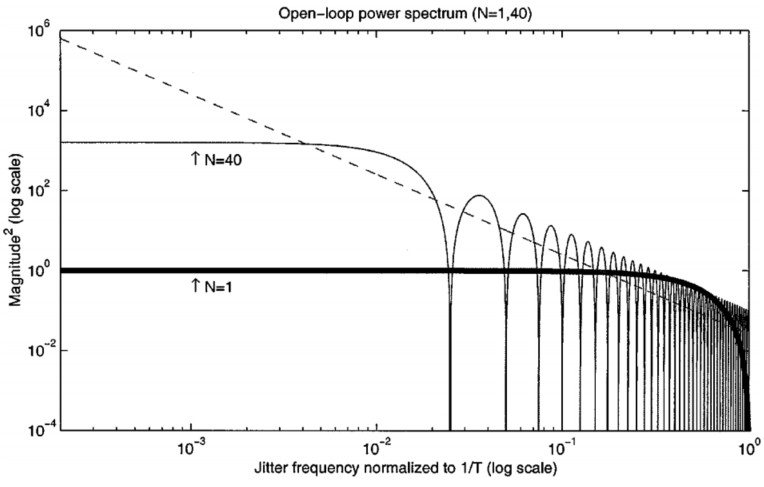
重要结论
所以这里我给出结论,在Bogdan的VHDL模型中,采用的是$N=1$的噪声功率谱密度情形,也就是Period Jitter;而在一般测量PLL的$Jitter_{rms}$时,我们采用的是$N=length(Data)$的方式进行测算的,所以Period Jitter由于自身携带了滤波效应,所以计算出的$Jitter_{rms}$自然就会小;而$N=length(Data)$的方式测算出的噪声功率谱密度曲线与绝对抖动的情形最为接近,滤波效应小,所以计算出的$Jitter_{rms}$比较大。
读者可以记住的结论是:$p_N(n)=x(n)-x(n-N)$一式中的N越大,其抖动越趋近于绝对抖动。N越小,低通滤波效应越强,抖动大小越小。

