写在前面
最近需要对ADPLL中的DCO进行时域建模,初步考虑采用Verilog-A进行时域模型建模,之前的模型产生了诸多问题,例如对于DCO的$\sigma_{jitter}$大小的设置,在网上查阅到相关的模型,这些模型对于$\sigma_{jitter}$都非常小。通过公式计算后得到,在我们的应用中,$\sigma_{jitter}=1fs$。但是我们的PLL输出的时钟的$\sigma_{jitter}$应该有$50fs$。为什么$1fs$的模型可以导致$50fs$的结果呢?这是我的疑问之一。
其次对于DCO输出质量的测量问题,我也不是很清楚,为此,我查阅了论文:
“Event-Driven Simulation and Modeling of Phase Noise of an RF Oscillator”
这篇论文内详细说明了DCO该如何进行时域建模,并且根据文献:
“Spectral Analysis of Time-Domain Phase Jitter Measurements”
以及文献:
“Experimental verification of the link between timing jitter and phase noise”
这两篇文献弄清楚了绝对抖动(Absolute Jitter)和周期抖动(Period Jitter)之间的关联与区别。如果对这些概念感兴趣的读者可以查阅我的阅读笔记:”时域抖动测量的谱分析”和”事件驱动型的仿真中的DCO相位噪声建模”两篇文章。
模型代码
//Verilog A for ADPLL, DCO_A, veriloga
`include "constants.vams"
`include "disciplines.vams"
// 下面的代码如果没有会出现错误如下:
// ERROR (SPECTRE-16041): Analysis was skipped due to inability to compute operating point.
nature Voltage
abstol = 1e-12;
access = V;
blowup = 1e308;
units = "V";
endnature
module DCO_A(OUT, VSS, VDD, IN_A, FREQ_A, dT_A);
electrical OUT, VSS, VDD, IN_A, FREQ_A, dT_A;
parameter real Fmin = 30G-1G from (0:inf);
parameter real Fmax = 30G+1G from (0:inf);
parameter real Vlo = 0, Vhi = 900m;
real jitter = 1f from [0:0.25/Fmax); // Period Jitter
real ttol = 1u/Fmax from (0:1/Fmax);
real FullRange = 2^7, Input_Value = 0;
real freq, phase, dT;
integer n, seed;
genvar i;
analog begin
@(initial_step) seed = -561;
$bound_step(0.6/freq);
// Generate the frequency using binary input data
Input_Value = V(IN_A);
// Calculate the output frequency
freq = 30G;
// Add the Phase Noise
freq = freq/(1+dT*freq);
// Perform circular integration idtmod(expr, ic, modulus, offset)
phase = 2*`M_PI*idtmod(freq, 0.0, 1.0, -0.5);
@(cross(phase + `M_PI/2, +1, ttol) or cross(phase-`M_PI/2, +1, ttol))begin
dT = $rdist_normal(seed, 0, jitter); //[Mean = 0; STD = 1]
n = (phase >= -`M_PI/2) && (phase < `M_PI/2);
end
//Generate Output
V(OUT) <+ transition(n ? Vhi : Vlo, 0, ttol);
V(FREQ_A) <+ freq;
V(dT_A) <+ dT;
end
endmodule
频率产生
// Add the Phase Noise
freq = freq/(1+dT*freq);
代码中的频率变化是通过如下的公式实现的,
$$
\Delta f = -f_0^2\Delta T
$$
上面的公式已经在本博客多篇相关的文章推导和出现过了,如果不清楚的读者可以回去翻看我先前的博客。这里仅仅对这一公式成立的条件做一个说明,该公式成立的条件是$\Delta T$要足够小,一般情况下在我们的ADPLL应用中通常是满足的。另外需要说明的是这里的符号问题,可以看到这里有一个负号,直观上的理解就是周期变长了,频率自然会变小,频率变化率为负值,这里就是负号的来源。
接下去推导代码中的公式,我们可以直接写出新频率的数学表达式,如下所示,
$$
f_{new} = f_0+\Delta f=f_0-f_0^2\Delta T=f_0(1-f_0\Delta T)
$$
又知有以下关系成立,
$$
1-f_0\Delta T\approx\frac{1}{1+f_0\Delta T}
$$
所以有,
$$
f_{new}=\frac{f_0}{1+f_0\Delta T}
$$
上式与代码中的公式是对应的。
相位产生和高低电平产生机制
本代码的相位信息是通过idtmod的函数实现的,通过此函数我们可以限制代码中变量的最大值,降低代码的空间复杂度。该函数的输出值域为$[-0.5, 0.5]$,再考虑乘上系数$2\pi$之后,最终的值域为$[-\pi,\pi]$,可以发现覆盖整个$2\pi$的范围的。
本代码的高低电平是通过cross结合@语句的判断方式实现的,代码如下所示,
@(cross(phase + `M_PI/2, +1, ttol) or cross(phase-`M_PI/2, +1, ttol))begin
dT = $rdist_normal(seed, 0, jitter); //[Mean = 0; STD = 1]
n = (phase >= -`M_PI/2) && (phase < `M_PI/2);
end
可以看到cross函数判断现在相位是否进行到从左向右穿过$-\frac{\pi}{2}$,或者从左向右穿过$\frac{\pi}{2}$。如果是,则需要产生对应的边沿抖动,并判断到底是生成上升沿还是下降沿,直观上可以如下图所示。
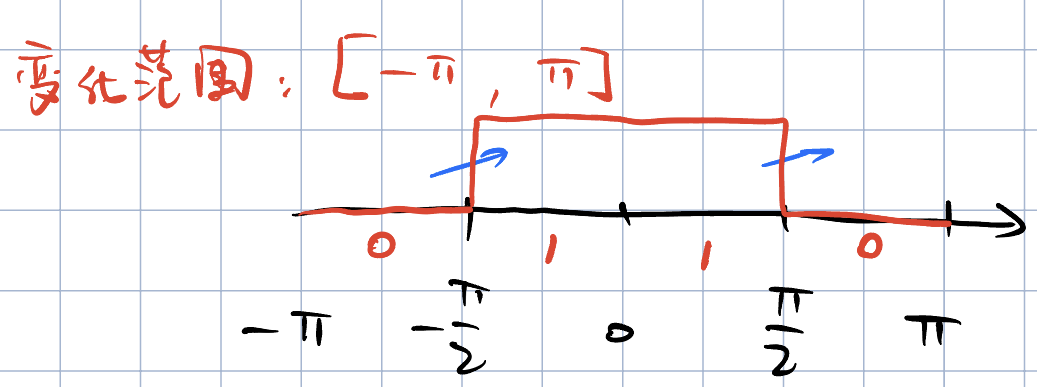
如果phase上穿$-\frac{\pi}{2}$,那么phase一定$\geq-\frac{\pi}{2}$并且$<\frac{\pi}{2}$,所以n为1;反之,n为0。这样我们就可以看到最终的0,1随相位的分布图如上图所示。
值得注意的是,这个模型的抖动是作用在周期上的,波形的占空比是严格的50%,时间戳的数学描述如下所示,
$$
t[i]-t[i-1]=T_0+TDEV[i]
$$
如何测量
根据该模型,我们产生的是方波数据,如何根据方波给出相位噪声功率谱密度呢?Bogdan在其论文:”Event-Driven Simulation and Modeling of Phase Noise of an RF Oscillator”中给出了一些提示。
方波的有用信息就是它的过零点,其过零点是确定的,假设第n个周期的上升沿时刻的时间戳为$t[n]$,我们可以把方波的这些时间戳全部取出来,假设我们的数据长度为$N=length(t)$,那么我们的平均周期为$T_0=(t[n]-t[1])/(N-1)$。有了这个信息之后就可以继续计算绝对抖动了,绝对抖动的表达式如下所示,
$$
TDEV[i]=t[i]-i\cdot T_0
$$
那么根据绝对抖动的值,通过关系$\Delta\phi=2\pi f_0\Delta t$,我们可以将时间抖动转换$TDEV$为相位噪声$\phi$,如下所示,
$$
\phi[i]=2\pi f_0TDEV[i]
$$
有了相位噪声信息之后,我们可以直接对相位噪声$\phi[n]$进行fft操作,绘制出$\phi[n]$的功率谱密度。
至此我们打通了Verilog-A代码到噪声功率密度谱的通道,为后期建模打下了坚实的基础。

