DCO的Verilog模型 | 古惑仔之家

ADPLL

发布日期: 2023-02-13

文章字数: 1.1k

阅读时长: 4 分

阅读次数:

写在前面

本文写Verilog模型，主要受到了两篇文章的启发，一篇是：

“Event-driven Simulation and modeling of phase noise of an RF oscillator”

还有一篇是复旦大学俞思辰的博士论文：

“无线射频领域中宽带全数字频率综合器的研究与设计”。

写在这里给需要的读者参考，并且向两篇论文的作者致谢，感谢他们给予我这个美妙的思路。

为什么要用Verilog？

Verilog模型是全数字建模模型，比较适合于数字电路，由于我们的Cadence中的电路大部分都是模拟电路，尽管如此，Cadence中也提供了数字电路的解决方案，那就是Verilog-A，这个语言模型能够帮助我们在模拟电路中快速建模数字电路。但是Verilog-A本质还是一个过采样的模型。

为什么我们不需要过采样呢？因为DCO模型中，我们每个周期的抖动都是确定的，由一个正态分布的随机数给定，在这个基础之上，我们根据窄带FM近似原理，只需要获取时钟上升沿或者下降沿的时间戳就可以获取整个电路的性能模型了。所以我们只关注时间戳，不关注其中的过程，根据这个说法，我们就不需要额外进行过采样的操作了，这样只会浪费我们的数据资源和计算资源。

Verilog就是基于边沿进行计算的仿真软件，因此，我们采用Verilog进行我们的模型的建模。如果从仿真时间角度进行分析，Verilog和Verilog-A仿真同样的模型，Verilog比Verilog-A仿真要快2~3个数量级。

Verilog代码

`timescale 1ps/1fs
module DCO_test #(
  parameter wander_rms = 0.70894,
  parameter jitter_rms = 0
) (
  input wire period0,
  input wire en,
  output reg clk
);
  reg smp = 0;
  real jitter=0;
  real jitter_prev=0;
  real wander = 0;
  real scale = 100;
  real period_nom = 33.33333333333;
  real period = 0;
  real randvar;
  real delay = 0;
  real half = 2;
  integer handle;
  integer seed = -561;

  initial begin
    handle = $fopen("zero_crossing.csv");

    clk = 1;
    delay = period_nom*scale/2;
    period = period_nom*scale;
  end
  
  always begin
    forever begin
        period = period_nom*scale;
        // randvar = $dist_normal(seed,0,jitter_rms*scale);
        // jitter = randvar;
        // period = period + jitter - jitter_prev;
        // jitter_prev = jitter;
        randvar = $dist_normal(seed,0,wander_rms*scale);
        wander = randvar/1000;
        period = period + wander;
        delay = period/half;
        // 下降沿
        #(delay);
        clk = smp;  // 1->0
        smp = ~smp;
        // 上升沿
        #(delay);
        $fdisplay(handle,"%.9f",$realtime/scale, ",", clk);
        clk = smp;  // 0->1
        smp = ~smp;
    end
  end
endmodule

上面给出了详细的Verilog建模的代码，在代码中给出标称周期以及Period Jitter的均方根值，我们就可以得到最终的数据，采用$fdisplay()函数将数据从Modelsim中转换到csv文件格式，并最终在MATLAB中进行数值分析。

杂散的来源

如果读者将scale设置为10，并且在$fdisplay中的参数设置为$time之后，读者就会发现在10GHz处会产生一个Spur，如下图所示，

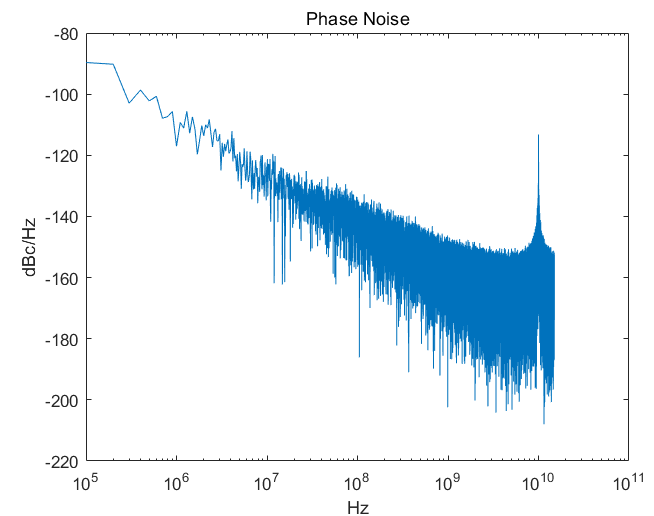
这大概是由于取整操作造成的，类似于DeltaSigma中的杂散。

如果读者将$fdisplay中的参数设置为$realtime之后，产生的相位噪声功率谱密度如下所示，

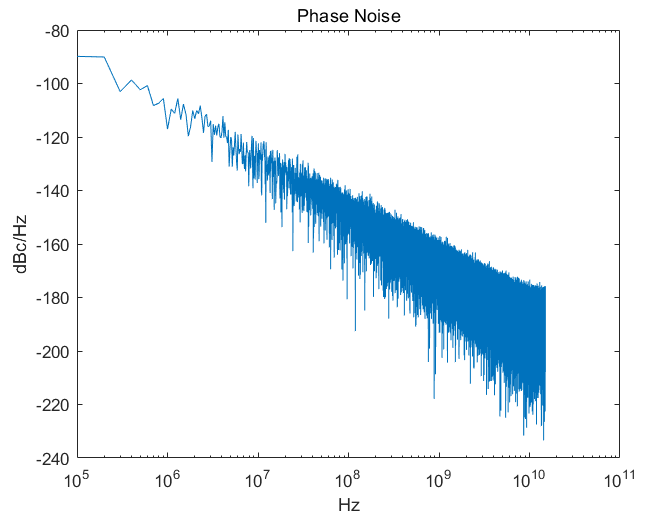
因此这个问题大概率是因为时间戳的时间精度不够造成的。（此处是我猜测的结论，没有确定的被验证）

MATLAB数据分析模块

clc;
clear;
filename = 'zero_crossing.csv';
data = csvread(filename,1,0);   
zerocrossings = data(:,1)./1e12;
N = length(zerocrossings);
TDEV = zeros(1,N);
T0_avg=(zerocrossings(N)-zerocrossings(1))/(N-1);
for i=1:N
    TDEV(i)=zerocrossings(i)-(i)*T0_avg;
end
phi=2*pi*(TDEV./T0_avg);
SpectrumSSB = FFTSpectrum(phi,1/T0_avg);
NoisePower = 0;
Expectation = 0;
for i = 6 :length(SpectrumSSB)
    NoisePower = NoisePower + SpectrumSSB(i)^2;
end
JitterRMS = sqrt(NoisePower/(2*pi/T0_avg)^2)
std(TDEV)
mean(TDEV)

上述主函数主要完成了数据的处理，转换，以及计算操作，获得最终的相位功率谱密度。具体的相位噪声功率谱密度由下面的函数代码进行执行，

function [SpectrumSSB] = FFTSpectrum(Signal,Fs)
    Signal_window = length(Signal)*1/Fs;
    Spectrum_Resolution = 1/Signal_window;
    Spectrum_Complex = fft(Signal);
    Spectrum_Magnitude_DSB = abs(Spectrum_Complex)/length(Signal);
    for i=2:length(Signal)/2
        % Pay Attention to sqrt(2). This is required due to magnitude
        % spectrum being added is equivalent to multiplied by sqrt(2)
        Spectrum_Magnitude_SSB(i) =  (Spectrum_Magnitude_DSB(i+1)+Spectrum_Magnitude_DSB(length(Signal)+1-i))/sqrt(2);
    end
    Spectrum_Magnitude_SSB(1) = Spectrum_Magnitude_DSB(1);
    L = 10*log10(Spectrum_Magnitude_SSB.^2/Spectrum_Resolution);
    semilogx((0:Spectrum_Resolution:length(Signal)/2*Spectrum_Resolution-Spectrum_Resolution),L);
    title('Phase Noise');
    xlabel('Hz');
    ylabel('dBc/Hz');
    SpectrumSSB = Spectrum_Magnitude_SSB;
end

基于上述操作，就可以完成数据相位噪声功率谱密度的评估工作。