写在前面
TTC(Time Transfer Constant)这个方法本人经过验证之后发现,非常有用,受益颇丰。本人先前分析类似电路时,总是遇到无从下手的情形,使用这个方法之后,分析电路非常迅速,可以迅速找到Dominant Pole、以及Zero的位置。并且其中的方法在许多论文中都有应用,在此罗列一下,以便之后参考。
本文的内容来源:Ali Hajimiri的视频课程:New Analog IC Design.
链接:https://www.youtube.com/watch?v=403CnTftB4M&list=PLc7Gz02Znph-c2-ssFpRrzYwbzplXfXUT
或者可以参考Ali Hajimiri的论文:
A. Hajimiri, “Generalized Time- and Transfer-Constant Circuit Analysis,” in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 57, no. 6, pp. 1105-1121, June 2010, doi: 10.1109/TCSI.2009.2030092.
从传输函数到零点极点分析
一般电路的传输函数如下所示,
$$
H(s)=\frac{a_0+a_1s+a_2s^2+···+a_ms^m}{1+b_1s+b_2s^2+···+b_ns^n}
$$
为了直观看到零点与极点,典型的电路的传输函数也可以写成下面的形式,将零点与极点写在分母上的好处是,$a_0$可以直接是DC增益。
$$
H(s)=a_0\frac{(1-\frac{s}{z_1})(1-\frac{s}{z_2})···(1-\frac{s}{z_m})}{(1-\frac{s}{p_1})(1-\frac{s}{p_2})···(1-\frac{s}{p_n})}
$$
如果极点满足以下条件,那么称$p_1$为Dominant Pole(主极点)。
$$
|p1|<<|p2|<<|p3|<<···
$$
观察第一个传输函数可知,$b_1$满足下面的关系,
$$
b1=-\Sigma_i\frac{1}{p_i}
$$
如果存在条件,$|p1|<<|p2|$,那么可以有下面的结论,
$$
b1\approx-\frac{1}{p_1}
$$
如果还存在条件,$|p2|<<|p3|$,那么可以有下面的结论,
$$
b2\approx\frac{1}{p_1p_2}
$$
总结一下就是,如果传输函数存在一个主极点(通常来说,设计好的电路都是这样的),那么我们的分母一次项的系数就是我们的主极点的倒数,同理,第二个主极点的位置就是主极点和非主极点的乘积的倒数。
ZVT,Zero Value Time Constant方法
这个方法在Paul Gray的书中有做介绍,但是书中的内容总是不够直观,看起来也比较枯燥。本文接下去的内容对这个方法进行了详细的描述。
我们先考虑只有一个Reactive Element的情况,也就是下面的两种情形,左图表示了只有电容的情形,右图表示了只有电感的情形。其中的大圈表示”No Dynamics”的电路部分,也就是说,其中没有电感和电容的部分。
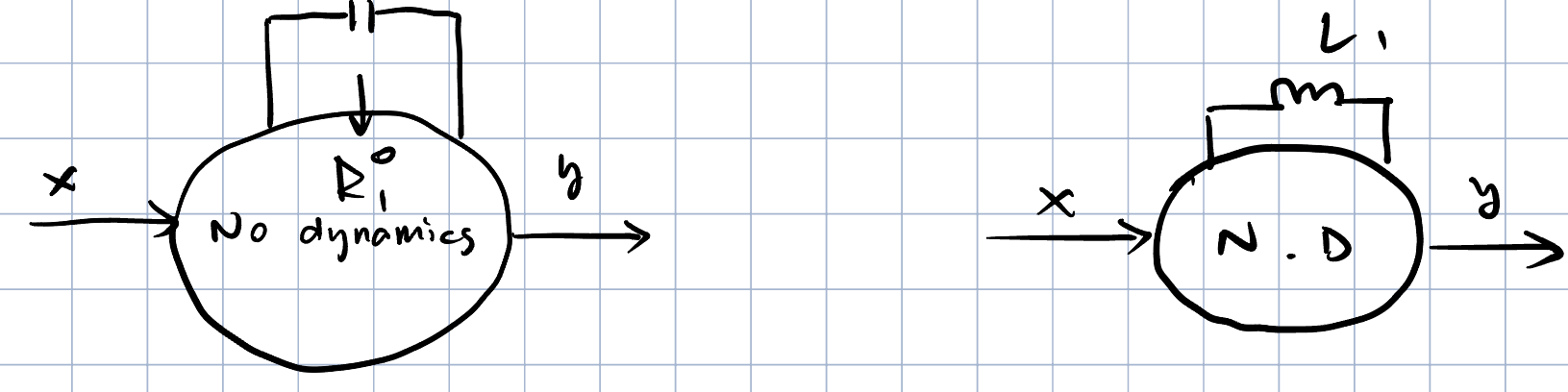
上面的电路只有一个Reactive Element,所以一定可以用下面的表达式进行表达,
$$
H(s)=\frac{a_0+a_1s}{1+b_1s}
$$
这里要介绍一个有限零点(Finite Zero)和无限零点(Infinite Zero)的概念,有限零点表示零点是一个有限的实频率,而无限零点表示零点为无穷大频率。直观来说,有限零点对应的情况为:$a_0\neq0$,$a_1\neq0$;而无限零点对应的情况是:$a_1=0$。这种无限零点的说法,在Ahuja的文章:
B. K. Ahuja, “An improved frequency compensation technique for CMOS operational amplifiers,” in IEEE Journal of Solid-State Circuits, vol. 18, no. 6, pp. 629-633, Dec. 1983, doi: 10.1109/JSSC.1983.1052012.
一文中,有无限零点、有限零点的这种说法存在,我怀疑Ahuja也是使用了这种方法进行电路零点极点分析的。
上面的表达式可以进一步写成如下的表达式,可以写成下面表达式的原因是因为我们的$s$永远是和$C_1$一起出现的,所以我们可以把包含$s$的项提出一个$C_1$出来。
$$
H(s)=\frac{a_0+\alpha_1^1C_1s}{1+\beta_1^1C_1s}
$$
$b_1$是我们的时间常数,$\tau=C_1R_1^0$。这里要说明一下我们的命名方式,这里除了下标,还会有上标,上标表示值为无穷的器件,也就是频率为无穷大时,器件的阻抗,这时,电容为短路,电感为开路,另外,如果上标为零,那么表示所有器件均为零值,也就是频率为零,DC时的情况,这时,电容为开路,电感为短路。根据这个描述,我\们可以把上面的表达式写成如下形式,
$$
H(s)=\frac{H^0+H^1R_1^0C_1s}{1+R_1^0C_1s}=\frac{H^0+H^1\tau s}{1+\tau s}
$$
几个例子
例子一
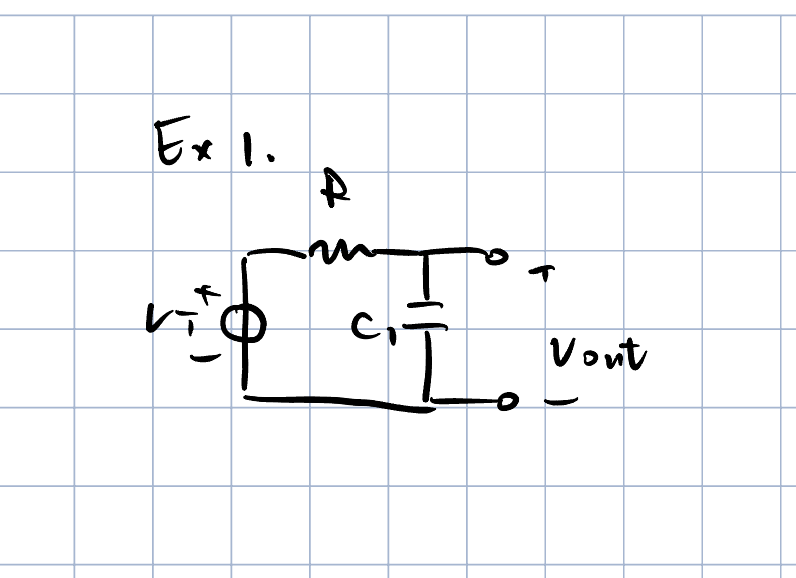
先计算$H^0$,也就是所有Reactive Elements的值为零的传输函数,换句话说,也就是所有电容开路,所有电感短路时的电路的传输函数。这时,输入直接传递到输出,没有衰减和增益,所以,
$$
H^0=1
$$
再计算传输函数$\tau_1^0$,计算这时的传输函数,要将除了$C_1$之外的电容全部开路,将所有独立电压源短路,所有独立电流源开路,求从$C_1$两侧看入的阻抗$R_1^0$的大小。从$C_1$只能看到$R$,所以,
$$
\tau_1^0=R_1^0C_1=RC_1
$$
再计算$H^1$的值,$H^1$是将$C_1$的值为无穷大,其他Reactive Element的值为0时,电路的传输函数,也就是将$C_1$短路时,电路的传输函数,这时,输出被短路,所以有,
$$
H^1=0
$$
综上所述,我们利用一开始的ZVT公式,可以得到如下的电路传输函数,
$$
H(s)=\frac{1}{1+RC_1s}
$$
到这里我们就推导了一阶RC低通滤波器的传输函数。
例子二
接下去我们看第二个例子
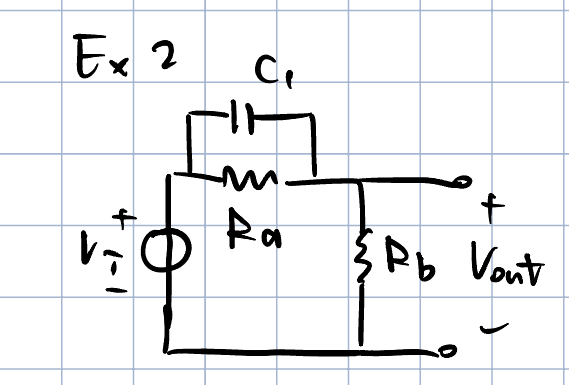
我们可以先计算一下该电路的DC增益:
$$
H^0=\frac{R_b}{R_a+R_b}
$$
接下去我们去计算我们的时间常数$\tau_1$,计算该时间常数的办法是,
- 将所有的源归零;
- 将其他的电抗器件的值变为零;
- 计算$C_1$两侧看入的电阻$R$,并与$C_1$相乘得到时间常数$RC_1$
$$
\tau_1=(R_a||R_b)C_1
$$
接下去我们计算$H^1$,计算$H^1$的办法就是将$C_1$的值变为无穷大,其他的电抗器件的值变为0,然后测算从输入到输出的增益。
这里,我们将$C_1$短路,获得的$H_1$如下所示,
$$
H_1=1
$$
所以,根据先前的公式,有,
$$
H_(s)=\frac{H^0+H^1\tau_1s}{1+\tau_1s}=\frac{\frac{R_b}{R_a+R_b}+(R_a||R_b)C_1s}{1+(R_a||R_b)C_1s}
$$
从上述表达式中,我们可以发现增益从低频的$\frac{R_b}{R_a+R_b}$移动到高频的$1$,也就是从$H^0$变为$H^1$。
例子三
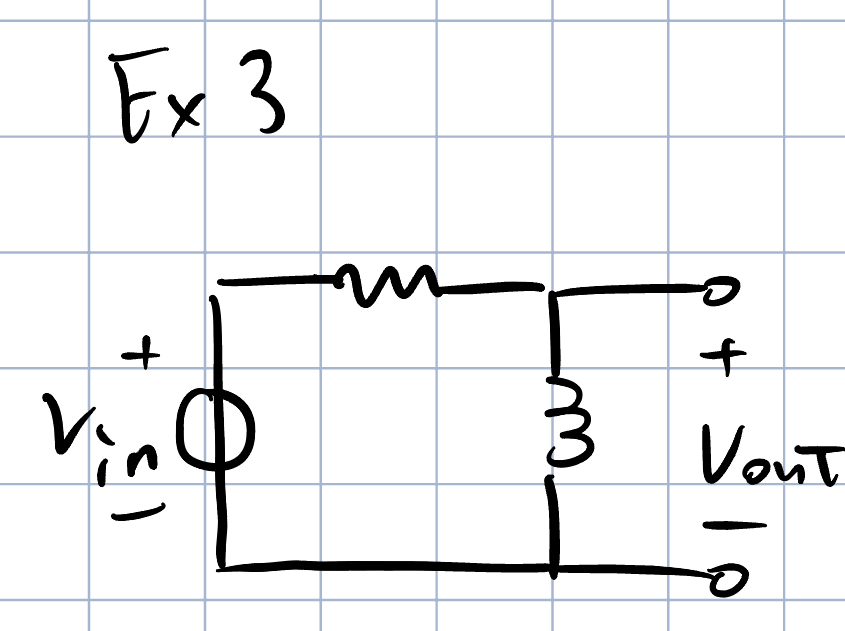
该例子中出现了电感器件,为了说明电感器件如何应用该理论,这里特别放置了这样的一个例子。首先说明,该电路为一阶RL高通滤波器。
我们先计算DC增益$H^0$,也就是所有的器件的值全部为零的情形,在该情形下,电感为短路,$sL=s\cdot 0=0$,电容为开路,$\frac{1}{sC}=\frac{1}{s\cdot 0}=\infty$。在这里,电感为短路,所以输出为零,即,$H^0=0$。接下去计算时间常数$\tau_1$,计算电感的时间常数和电容不同,电感的时间常数为$\frac{L}{R}$,所以有,
$$
\tau_1=\frac{L_1}{R}
$$
接下去我们继续计算$H^1$,即$L_1$器件的值为$\infty$时,电路的增益,这时电感为开路,输出增益为1,所以,
$$
H^1=1
$$
将上述表达式代入TTC公式中,可以得到如下的表达式,
$$
H(s)=\frac{\frac{L_1}{R}s}{1+\frac{L_1}{R}s}
$$
可以看到的是,该电路的传输函数是一个高通滤波器。
例子四
在案例四中,我们加入了受控源结构,即MOS管,使得问题与实际问题更加贴切,让我们来看看在MOS管中如何利用TTC理论。
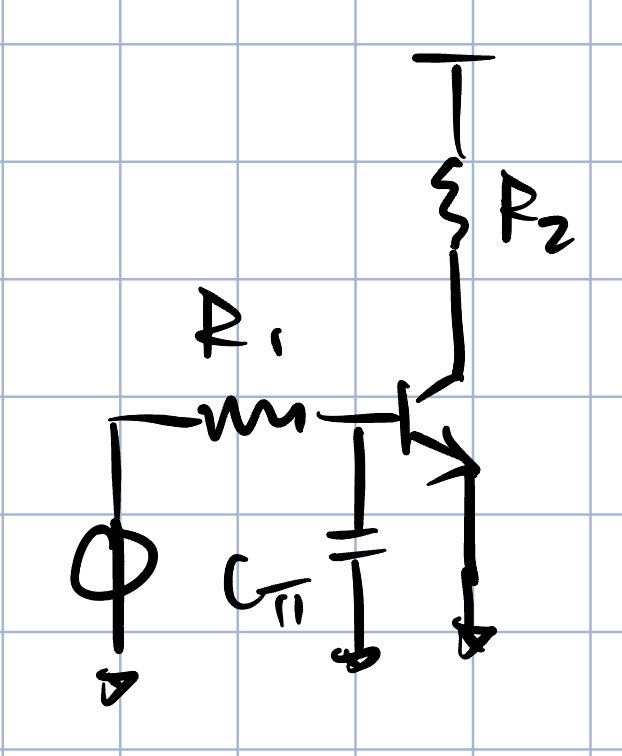
上图中的MOS管电路是一个共源放大器,我们可以先计算一下DC增益$H^0$,该增益由下式描述,
$$
H^0=-g_mR_2
$$
再来计算由$C_\pi$贡献的时间常数$\tau_\pi^0$,
$$
\tau_\pi^0=R_1C_\pi
$$
当我们想要计算$H_\pi$时,会发现当$C_\pi$短路时,该电路的增益为零,因为输入被短接到地了,所以有,
$$
H^\pi=0
$$
综上所述,我们可以得到总体的传输函数表达式,
$$
H(s)=\frac{-g_mR_2}{1+R_1C_\pi s}
$$
从这个例子中我们可以得到结论,如果短路电容或者开路电感,输出有且不为零,那么就存在一个零点;如果前后传输函数的极性被翻转了,那么就存在一个右半平面的零点,反之,如果传输函数的极性没有被翻转,那么就存在一个左半平面的零点。
一阶TTC在MOS管中的应用
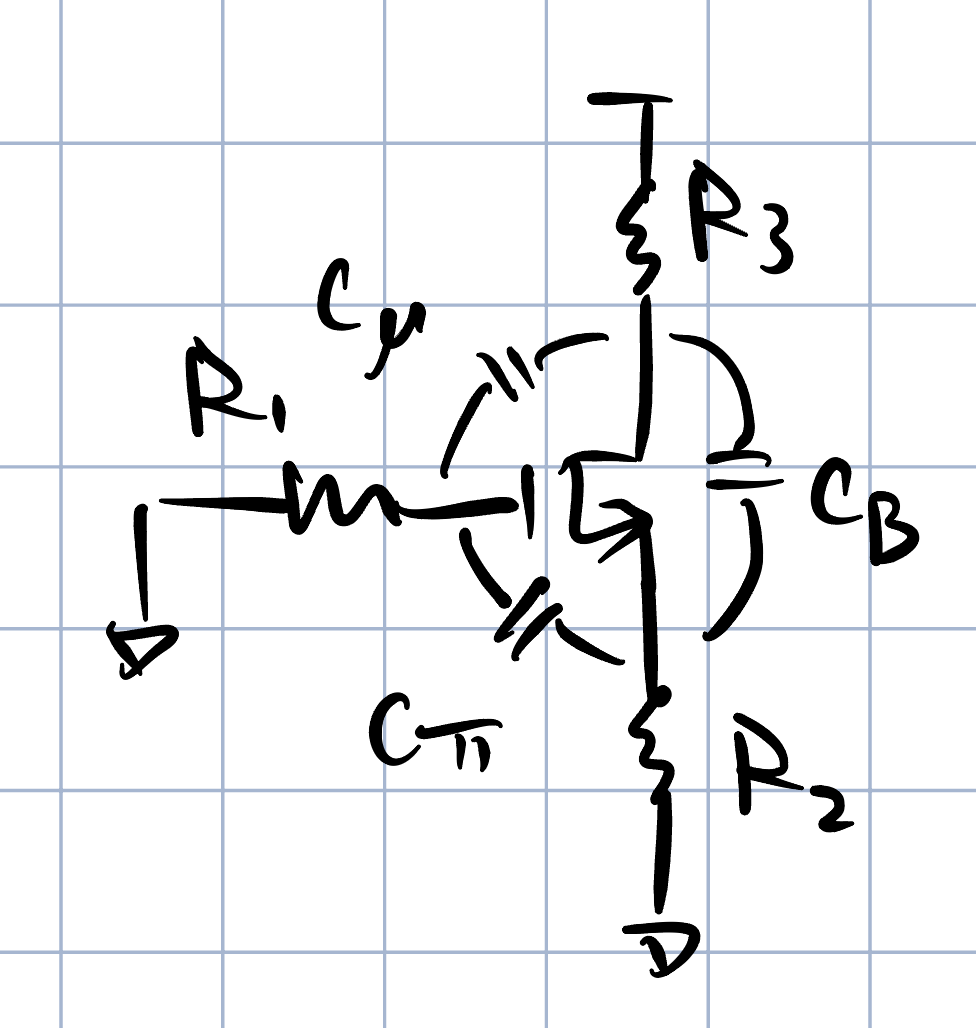
上述电路结构是一个典型的MOS管的寄生结构,该结构是一个通用的寄生模型,该模型在计算时间常数时,如果采用通常的小信号方法进行硬解,比较复杂麻烦,这里,给出了几个结论,并且给出了这几个结论的推导过程。
$R\mu$的计算方法
先给出结论,
$$
\tau_\mu^0=R_\mu C_\mu=(R_{left}+R_{right}+G_mR_{left}R_{right})C_\mu
$$
这里的$G_m$为等效跨导,该由于MOS管的源通常会接电阻,所以MOS管的跨导会发生退化,也就是源退化电阻导致的MOS管的跨导的减小。
下面对上面的结论进行推导,我们先给出了如下的电路图,
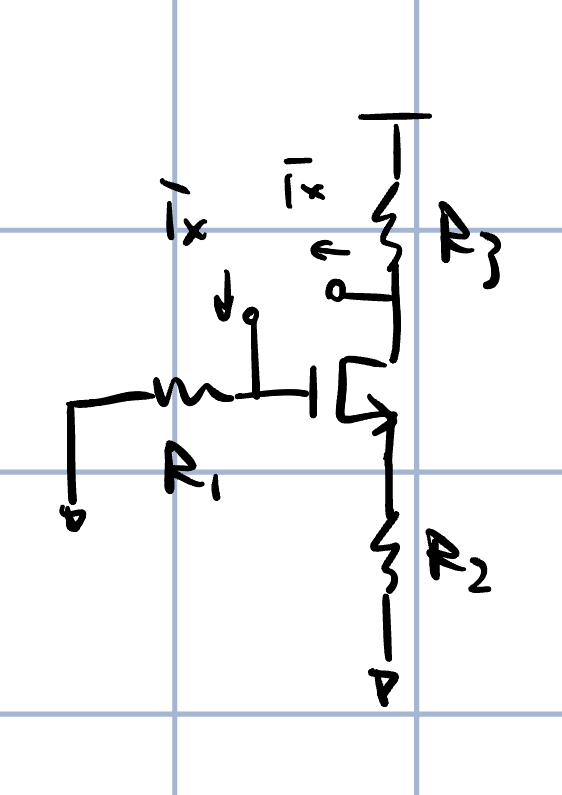
我们要测量$C_\mu$两端看去的阻抗,可以将$C_\mu$替换为电流源,电流为$i_x$,如上图所示,这样,这个电流会在栅上产生一个恒定的电压$v_g=i_xR_1$。
我们令流过管子的电流为$i_d$,这样,源上的电压为$v_s=i_dR_2$,我们接下去可以利用管子的跨导将栅源电压差和漏电流的关系表示出来,如下所示,
$$
(i_xR_1-i_dR_2)g_m=i_d
$$
化简之后,可以获得$i_d$与$i_x$之间的关系,如下所示,
$$
i_d=\frac{i_xg_mR_1}{1+g_mR_2}
$$
我们可以先观察一下上面的表达式,很明显有一个负反馈的意思在其中,这里的环路增益是$g_mR_2$。环路也比较明晰,栅电压升高$v_g$,产生更大的漏电流$v_gg_m$,进一步在源上产生电压$v_gg_mR_2$,通过$v_{gs}$反馈到输入上,具体的反馈图如下图所示,
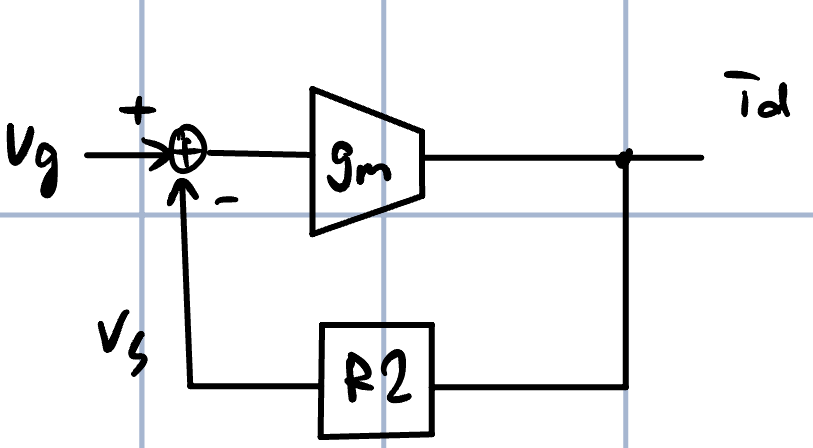
我们可以利用这个电流关系进一步计算$v_d$的表达式,如下所示,
$$
v_d=-idR_3-ixR_3=-\frac{i_xg_mR_1R_3}{1+g_mR_2}-ixR_3
$$
进一步我们可以得到最终的$v_x$电压,该电压的大小由下式表达,
$$
v_x=v_g-v_d=i_xR_1+\frac{i_xg_mR_3R_1}{1+g_mR_2}+i_xR_3=i_x(R_1+R_3+G_mR_1R_3)
$$
其中真正的跨导被源退化电阻缩小$g_mR_2$倍,所以为等效跨导。至此我们推导了$R_\mu$的大小。
$R\pi$的计算方法
先给出结论,$R_\pi$的计算方法如下,
$$
R_\pi=\frac{R_1+R_2}{1+g_mR_2}
$$
下面我们对该阻抗的计算方法进行一个推导,本质上就是计算如下图所示的端口看入的阻抗。
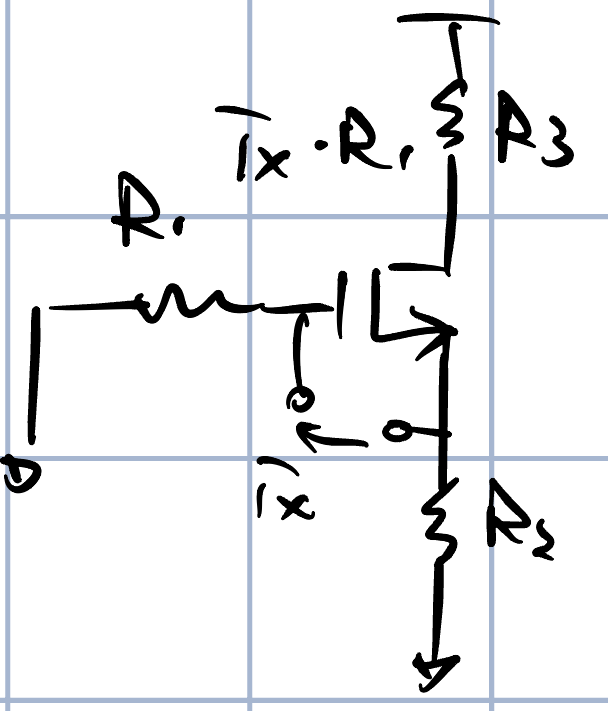
我们先解出$i_d$和$i_x$的关系,如下所示,
$$
(i_xR_1-i_dR_2+i_xR_2)g_m=i_d
$$
简单化简一下,我们可以得到下面的关系,
$$
i_d=\frac{g_m(R_1+R_2)}{1+g_mR_2}i_x
$$
接下去我们就可以解出$v_x$的大小,$v_x=v_{gs}$,如下,
$$
v_x=i_x(R_1+R_2)-\frac{g_m(R_1R_2+R_2^2)}{1+g_mR_2}
$$
化简有如下表达式,
$$
v_x=\frac{R_1+R_2}{1+g_mR_2}
$$
$R_B$的计算办法
$R_B$的计算方法与结果与$R_\pi$基本一致,表达式如下所示,这里就不做推导了。
$$
R_B=\frac{R_2+R_3}{1+g_mR_2}
$$
MOS管从源看入的阻抗表达式中的零点问题
如下图所示,我们可以看到一个典型的MOS管配置在源跟随器状态下的电路图,这时,MOS管存在寄生电容$C_\pi$,会产生一个阻抗的零点,下面对这个零点的来源进行一个推导。
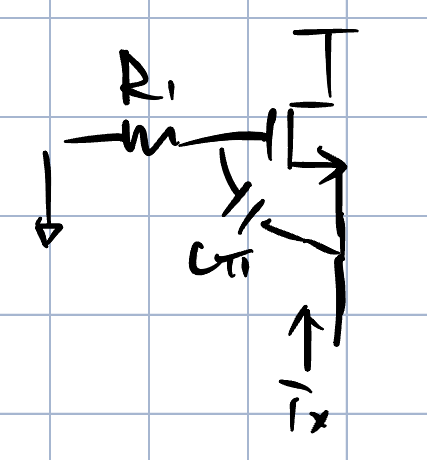
我们要计算输出阻抗,所以激励一定是电流,我们在源上施加一个流入的电流$i_x$。
我们先计算DC阻抗$Z^0$,这时,所有的电容的值均为零,也就是电容的阻抗为无穷大,即所有电容开路,这时的DC阻抗就是$1/g_m$,即,
$$
Z^0=1/g_m
$$
我们再去计算$Z^\pi$,即当$C_\pi$的值为无穷大时,这时看入的阻抗。这时,由于MOS管的栅和源之间被短路了,所以MOS管的源不能流入和流出电流,电流只可以流向$R_1$,所以,最终看入的阻抗为$R_1$,即,
$$
Z^\pi=R_1
$$
接下去我们需要计算时间常数$\tau_\pi^0$,计算这个时间常数主要是需要计算从$C_\pi$两侧看入的阻抗$R_\pi^0$,该阻抗在$R_1$以及$R_2$均为有限值时,由下式表达,
$$
R_\pi^0=\frac{R_1+R_2}{1+g_mR_2}
$$
但在本电路中,由于MOS管的源是开路的,所以,$R_2\rightarrow\infty$,所以,
$$
R_\pi^0=\frac{1}{g_m}
$$
根据上面的信息,我们已经可以写出s域下的阻抗表达式了,如下所示,
$$
Z(s)=\frac{Z^0+Z^\pi\tau_\pi^0s}{1+\tau_\pi^0s}=\frac{1/g_m+R_1C_\pi1/g_ms}{1+C_\pi1/g_ms}=\frac{1+R_1C_\pi s}{g_m+C_\pi s}
$$
从上面的阻抗表达式中,我们可以发现阻抗在低频的位置处,为$1/g_m$,到了高频处,为$R_1$。在一些对高频输出阻抗敏感的应用中,我们需要对电路的栅电阻尤为注意,要在此处加足够的Decap,否则,将会出现输出阻抗peaking的问题。
米勒电容问题
如下图所示,是一个米勒电容的模型,该电容跨接在电容的源和漏之间,形成了一个极点加上一个右半平面的零点。下面利用TTC推导上述结论,并且对零点和极点位置进行定量分析。
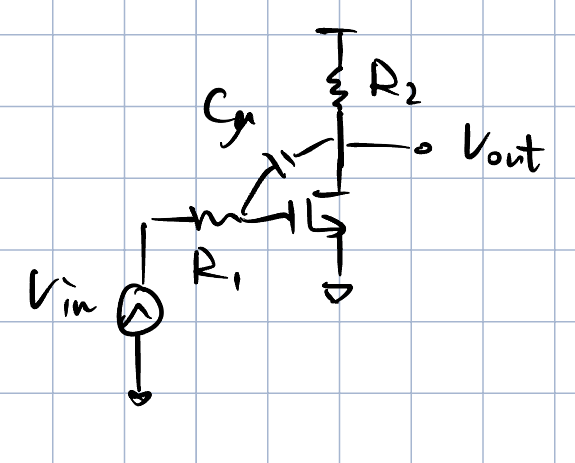
首先,先分析DC增益,DC增益为电容开路时,电路的增益,那么就是一个共源放大器的增益,如下所示,
$$
H^0=-g_mR_2
$$
接下去我们计算$H^\mu$,也就是当$C_\mu$的值为无穷大时,电路的增益,也就是当$C_\mu$短路时,电路的增益。当电容短路时,电路表现为输出经过$R_1$后,再与$R_2||1/g_m$串联分压,因此,增益表现为如下表达式,
$$
H^1=\frac{1/g_m||R_2}{R_1+1/g_m||R_2}=\frac{R_2}{R_1+R_2+g_mR_1R_2}=\frac{R_2}{R_\mu^0}
$$
注意上式中的$R_\mu^0$为$C_\mu$两端看到的阻抗。
所以电路的传输函数可以表示为如下所示,
$$
H(s)=\frac{H^0+H^1C_\mu R_\mu^0s}{1+C_\mu R_\mu^0s}=\frac{-g_mR_2+R_2C_\mu s}{1+R_\mu C_\mu s}=-g_mR_2\frac{1-C_\mu/g_m s}{1+R_\mu C_\mu s}
$$
从上面的表达式中,可以看到该电路中的极点为$-\frac{1}{R_\mu C_\mu^0}$,电路的零点为$\frac{g_m}{C_\mu}$。值得注意的是,这里的零点为右半平面零点,右半平面一方面会让增益以$+20dB/dec$的速度滚升,另一方面还会将相位降低$90\degree$。直观来说,对相位裕度有十分恶劣的影响,因为我们希望增益在到达$-180\degree$前滚降到0dB。我们来大概估计一下这个零点的位置,假设MOS管本身的寄生为$C_\mu$,那么最终的零点位置其实是比$f_T$要远的,这就意味着,一般情形下,零点位于GBW外。因此,在不额外增加电容的前提下,我们不需要关注这个零点对电路造成的影响。
零点的位置估计
从上面的内容中,我们不难发现,零点的计算方法如下,
$$
Z=\frac{H^0}{H^1}P
$$
仔细观察一下上面的式子,读者就会发现,零点实际上是极点位置经过修正后的结果。所以,只要知道修正系数的大小,我们就可以马上推算出零点的位置了。
下面我们给出一个相关的表格,来分析一下各种情况:
| 0 | $\frac{H^0}{H^1}<1$ | $\frac{H^0}{H^1}>1$ |
|---|---|---|
| $\frac{H^0}{H^1}>0$ | 零点极点位于同一平面 $|Z|<|P|$ |
零点极点位于同一平面 $|Z|>|P|$ |
| $\frac{H^0}{H^1}<0$ | 零点极点位于不同平面 $|Z|<|P|$ |
零点极点位于不同平面 $|Z|<|P|$ |
下图总结了上面不同的零点和极点关系对应的不同的频率响应。
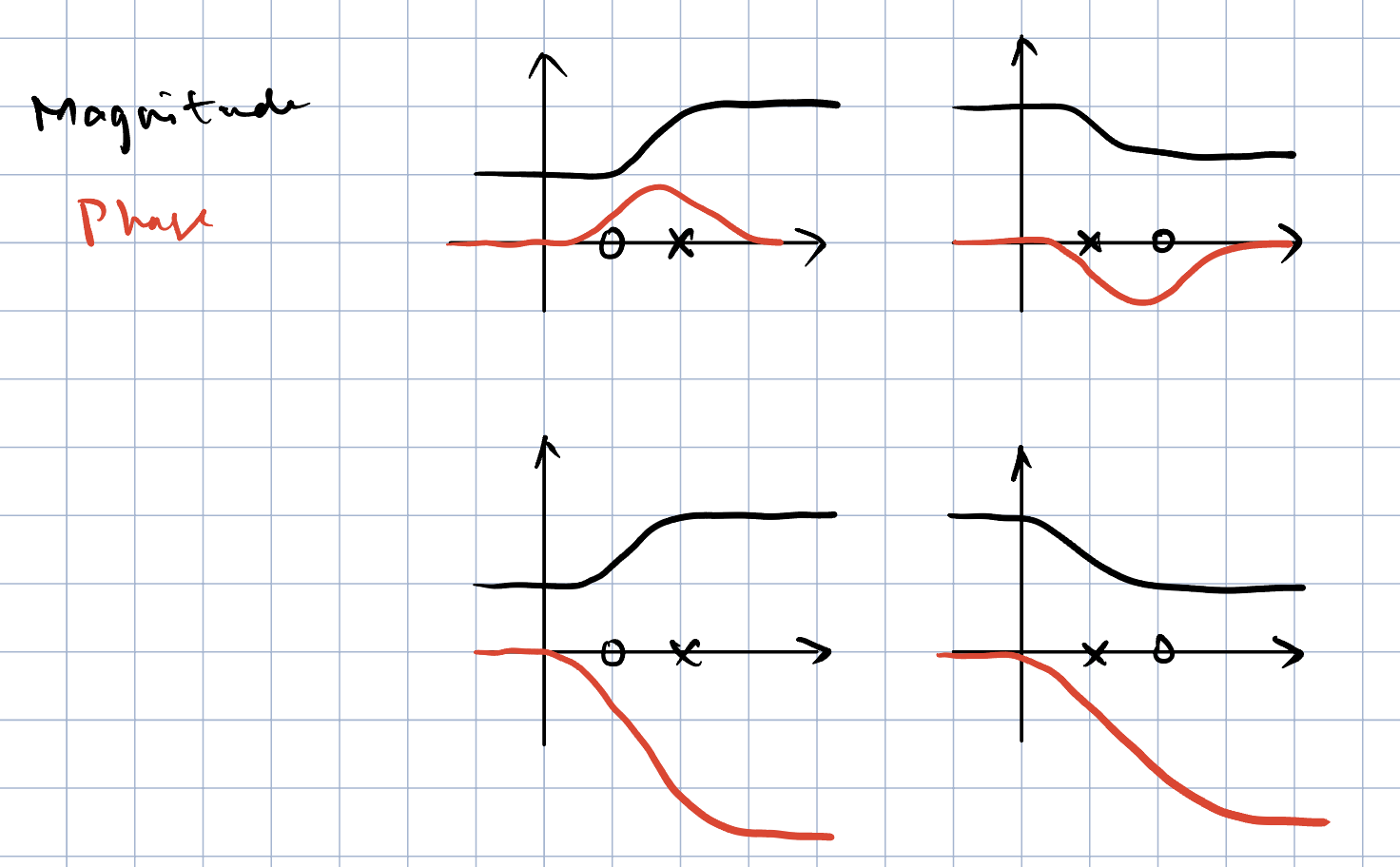
对于上面的一个极点一个零点的系统,我们可以对其进行分解,得到对应的时域响应表达式,如下所示,
$$
H(s)=\frac{H^0+H^1\tau s}{1+\tau s}=H^0\frac{1}{1+\tau s}+H^1\frac{\tau s}{1+\tau s}
$$
上式对应的时域表达式如下所示,
$$
h(t)=H^0(1-e^{-t/\tau})u(t)+H^1e^{-t/\tau}u(t)
$$
上述表达式的时域波形可以分解为如下图所示的图像,

可以看到的是,左半平面零点对应的时域响应是上述两个相应的和,将这两个响应相加,会发现如果$H^1$比较大,那么相应会有过冲的现象,如下图所示,
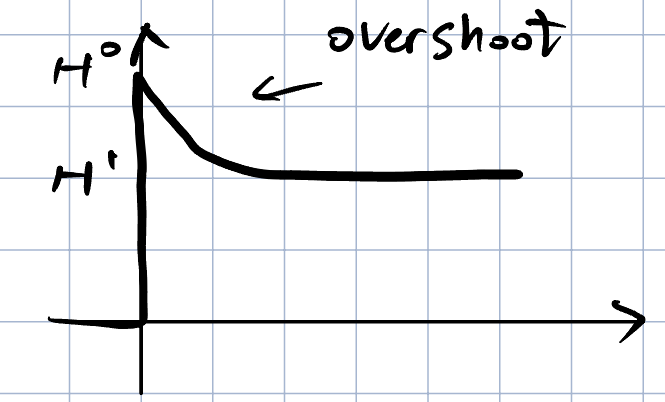
因此,需要注意的是,当读者看到阶跃响应出现过冲时,不仅仅会在二阶系统中出现,也有可能在一阶系统中出现。
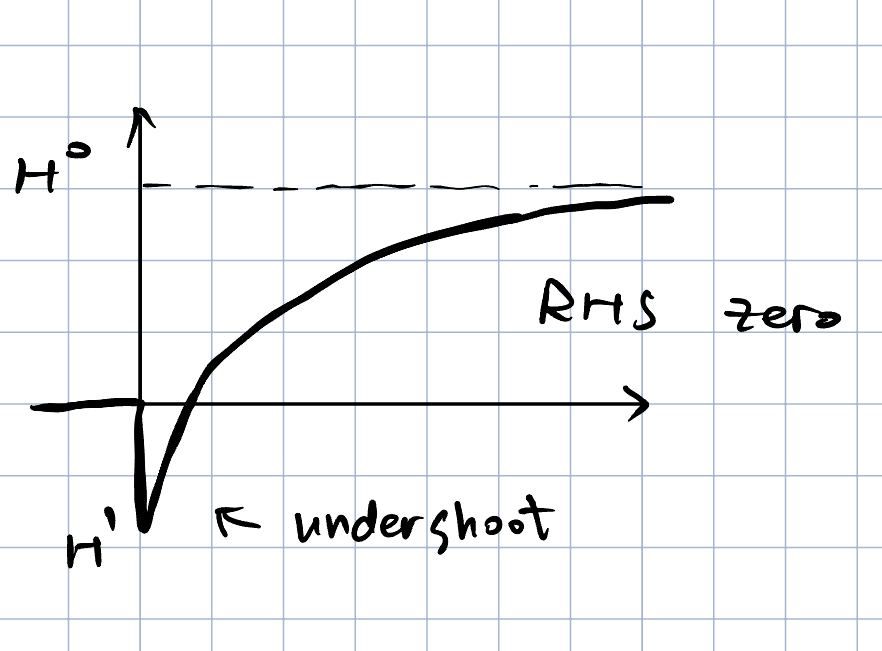
另一方面,如果电路中存在右半平面零点,那么该电路会有undershoot现象,如下所示,