写在前面
最近有一个需求需要做一个低压带隙基准,本人之前制作的带隙基准都是高压带隙基准,输出的电压都是1.25V的带隙电压,这次突然要做一个低压带隙基准,对本人也是一种考验。于是,我调研了低压带隙基准,根据如下论文进行了设计工作,参考文献如下,
B. Razavi, “The Design of a Low-Voltage Bandgap Reference [The Analog Mind],” in IEEE Solid-State Circuits Magazine, vol. 13, no. 3, pp. 6-16, Summer 2021, doi: 10.1109/MSSC.2021.3088963.
普通带隙基准是如何工作的?
带隙基准的目的就是获得一个与温度无关的电压,我们利用一个与温度成反比的NTAT电压,加上一个与温度成正比的PTAT电压,就可以获得一个与温度无关的CTAT电压。这里简单说明正温度系数电压和负温度系数电压都是怎么获得的。
负温度系数电压
负温度系数电压利用的三极管的VBE电压,如下图所示,
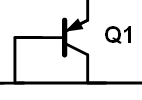
这个电压也就是二极管的正向电压,具有负温度系数。下面,具体说明这个电压是如何与温度负相关的。对于一个三极管器件,我们熟悉其特性曲线的表达式,如下所示,
$$
I_C=I_Se^{\frac{V_{BE}}{V_T}}
$$
其中的$V_T=kT/q$为热电压,这时我们可能会说,诶,这个为了保持一定的电流,那么$V_{BE}$应该和温度成正比呀?我第一次看到这个表达式的时候,也会有这样的疑问,但是实际上,我们忽略了$I_S$饱和电流的这一参数的影响,该参数与$\mu kTn_i^2$成正比。这些参数对于读者来说都是魔法参数,需要与我们所关注的温度相挂钩,这里给出这些参数与温度的关系。首先是我们的$\mu$,也就是少数载流子迁移率,与温度的关系如下所示,
$$
\mu\propto\mu_0T^m,m\approx-3/2
$$
接下去是$n_i^2$,$n_i$是硅的本征载流子浓度,这个参数与温度的关系如下所示,
$$
n_i^2\approx T^3e^{-\frac{E_g}{kT}}
$$
其中,$E_g\approx 1.12eV$,为硅的带隙能量。把上述关系写入我们的三极管特征方程中,有如下关系,
$$
I_S=bT^{2.5}e^{-\frac{Eg}{kT}}
$$
由于我们刚才给出的是这些参数与温度的关系,因此,b是一个不包含温度的比例系数。我们需要计算$V_{BE}$与温度的关系,从数学角度来说,也就是希望计算$\frac{\partial V_{BE}}{\partial T}$,所以我们给出$V_{BE}$的表达式,如下所示,
$$
V_{BE}=V_Tln\frac{I_C}{I_S}
$$
接下去我们就是要将上面的表达式的$V_{BE}$对温度$T$求导,利用乘法求导法则,如下所示,
$$
\frac{\partial V_{BE}}{T}=\frac{\partial V_T}{\partial T}ln\frac{I_C}{I_S}+V_T\frac{I_S}{I_C}\cdot(-\frac{I_C}{I_S^2})\frac{\partial I_S}{\partial T}=\frac{\partial V_T}{\partial T}ln\frac{I_C}{I_S}-\frac{V_T}{I_S}\frac{\partial I_S}{\partial T}
$$
上面的式子归根到底需要求两个导数,一个是$\frac{\partial V_T}{\partial T}$,还有一个是$\frac{\partial I_S}{\partial T}$,根据我们前面的分析,$\frac{\partial V_T}{\partial T}$的表达式如下所示,
$$
\frac{\partial V_T}{\partial T}=\frac{k}{q}
$$
$\frac{\partial I_S}{\partial T}$的表达式略微复杂,如下所示,
$$
\frac{\partial I_S}{\partial T}=2.5bT^{1.5}e^{\frac{-E_g}{kT}}-bT^{2.5}\frac{E_g}{kT}e^{\frac{-E_g}{kT}}
$$
整理上面的式子,我们可以得到最终的表达式,如下所示,
$$
\frac{\partial V_{BE}}{\partial T}=\frac{V_{BE}-2.5V_T-Eg/q}{T}
$$
这个值本质上与$V_{BE}$的大小有关,当$V_{BE}\approx800mV$,在室温下,$V_T=\frac{kT}{q}=\frac{1.380649e-23\times 300}{1.602e-19}\approx25.84mV$,$E_g=1.12eV$,将上述表达式的值带到上述等式中,可以得到$V_{BE}$关于温度的一阶导数为,$\frac{\partial V_{BE}}{\partial T}=-1.282mV/K$。
值得注意的是,上述三项中,中间一项$-2.5V_T/T$是可以忽略的一项,$V_{BE}/T$贡献$2.5mV/K$的正向变化,$-E_g/q/T=-1.12V/300K\approx-4mV/K$贡献了$-4mV/K$的负向变化。所以,如果忽略中间项的话,那么总的导数为$-1.5mV/K$。
正温度系数电压
正温度系数由两个$V_{BE}$的差值得到,如果两个晶体管的电流密度不同,那么,他们$V_{BE}$的差值就与绝对温度成正比,如下所示,
$$
\Delta V_{BE}=V_{BE1}-V_{BE2}=V_Tln\frac{nI_0}{I_{S1}}-V_Tln\frac{I_0}{I_{S2}}=V_Tlnn
$$
接下去,为了获得$\Delta V_{BE}$与温度的关联,将$\Delta V_{BE}$对$T$求导,如下所示,
$$
\frac{\partial \Delta V_{BE}}{\partial T}=\frac{k}{q}lnn
$$
先估算一下$\frac{k}{q}$的大小,如下所示,
$$
\frac{k}{q}=87uV/K
$$
获得恒定温度系数的电压和
通过上面的$V_{BE}$和$\Delta V_{BE}$的结合,适当放大$\Delta V_{BE}$,就可以得到恒定温度系数的量,如下所示,
$$
V_{out}=V_{BE}+\Delta V_{BE}\cdot N
$$
将上述式子对温度求导,如下所示,
$$
\frac{\partial V_{out}}{\partial T}=-1.5mV/K+N\cdot 87uV/K=0
$$
计算得到$N=17.24$
普通带隙基准电路
普通的带隙基准电路如下图所示,电路通过运算放大器和顶部的电流镜,强制左右两路的电流完全相同,并且强制X、Y两点的电压一致。
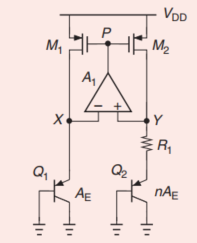
那么落在电阻$R_1$上的电压就是两个$V_{BE}$的差值,这样Y点的电压就是$\Delta V_{BE}+V_{BE2}$,通常为了保证$V_Y$电压对温度的导数为零,需要将$\Delta V_{BE}$乘以一个倍数$N$,假设这里的晶体管的电流密度的比例为$n=ln15\approx2.7$,为了保证恒定的输出电压系数,我们需要$N=\frac{17.24}{2.7}\approx6.37$,因此,通常的做法是在运放正负输入和电流镜之间,放置一个电阻,通过电阻的方式实现这个倍数。这个输出电压的大小如下所示,
$$
V_{out}=V_{BE}+17V_T\approx1.2
$$
上面的值差不多就是硅的带隙电压,因此,该基准称为带隙基准也正是基于这个原因。但是读者可以发现,该电压是一个比较高的电压,在低于1.2V供电的电路中无法进行实现,因此需要一个低压电路以实现这个电压。
低压带隙基准
下面的电路通过产生一个恒定的电流来产生一个恒定的电压,避免了直接产生恒定电压,从而规避了需要高供电电压的问题。
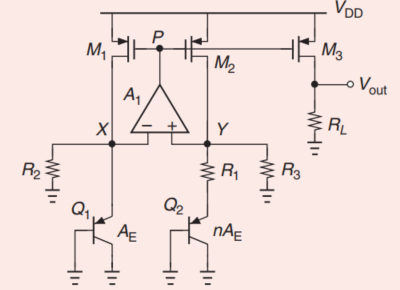
上述电路的工作原理是,通过运算放大器保证$V_X=V_Y$,因此,$I_{D2}=\frac{\Delta V_{BE}}{R1}+\frac{V_{BE}}{R_3}$,通过电流镜镜像到$M3$上,从而产生对应的电压$V_{out}$,如下所示,
$$
V_{out}=(\frac{\Delta V_{BE}}{R1}+\frac{V_{BE}}{R_3})R_L
$$
从上述表达式中可以看出,$\Delta V_{BE}$与$V_{BE}$之间的比例通过$R_1$和$R_3$两个电阻进行控制。因此,如果要获得恒定的输出电压,需要下面的式子成立,
$$
\frac{R_3}{R_1}lnn=17.24
$$
上述电路和分析可以使得读者自行制作一个低电压的Bandgap。

