写在前面
先直接给出Leeson-Cutler相位噪声模型的表达式,如下所示,
$$
L(\Delta \omega)=10\cdot log{\frac{2FkT}{P_s}\cdot[1+(\frac{\omega_0}{2Q_L\Delta\omega})^2]\cdot(1+\frac{\Delta\omega_{1/f^3}}{|\Delta\omega|})}
$$
其中
- $F$是一个经验参数(device excess noise number),AI给出的这个参数的大致范围是0.5~2.0;
- $k$是玻尔兹曼常数(1.38e-23);
- $T$是绝对温度;
- $P_s$是在tank里的电阻部分消耗的平均功率;
- $\omega_0$是震荡频率;
- $Q_L$是tank的有效品质因数,之所以称之为有效因为这时所有的负载全部加在这个上面,AI告诉我这个值大概是10~100;
- $\Delta\omega$代表了频率偏移主频的值;
- $\Delta\omega^3_{1/f}$代表了$1/f^3$区域与$1/f^2$区域的交界区域,如下图所示;
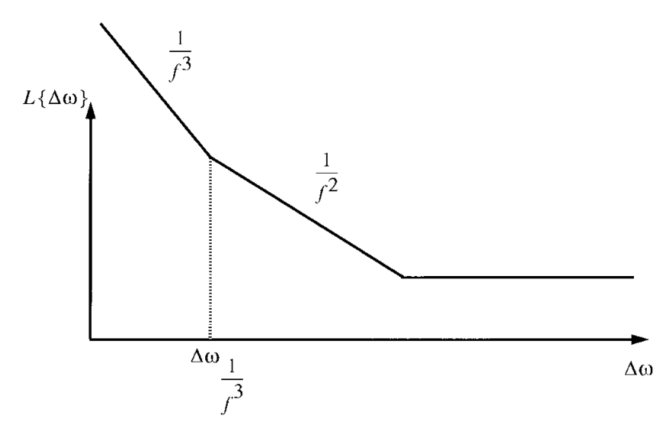
$1/f^2$区域的噪声
该区域的噪声可以通过下面的模型进行建模,先考虑一个RLC并联电路的输入阻抗,
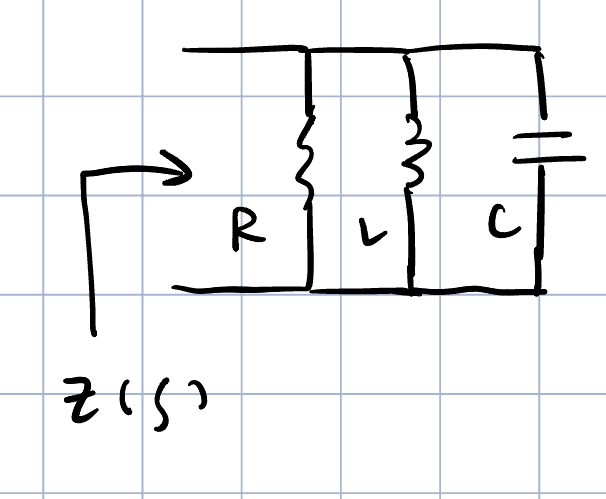
上述电路的阻抗$Z(s)$由下面的表达式表达,
$$
Z(s)=\frac{1}{1/R+1/sL+sC}
$$
通分化简后得到下面的表达式,
$$
Z(s)=\frac{sLR}{sL+R+s^2LCR}
$$
因为我们考虑的频率是$s=j(\omega_0+\Delta \omega)$,并且中心频率为$\omega_0=1/\sqrt{LC}$,将上述两个关系代入到我们的阻抗表达式中进行化简,
$$
Z(s=\omega_0+\Delta\omega)=\frac{j(\omega_0+\Delta \omega)LR}{j(\omega_0+\Delta\omega)L+R-\omega_0^2LCR-2\omega_0\Delta\omega LCR-\Delta\omega^2LCR}
$$
考虑到$\Delta\omega<<\omega_0$,所以,$\Delta\omega^2LCR$的一项可以被忽略;另一方面,由于$\omega_0^2=1/LC$,所以$-\omega_0^2LCR=-R$与前面的一项$R$抵消;并且,$-2\omega_0\Delta\omega LCR=2\Delta\omega R/\omega_0$。经过上述三步的化简,得到下面的表达式,
$$
Z(\omega_0+\Delta\omega)\approx\frac{j(\omega_0+\Delta \omega)LR}{j(\omega_0+\Delta \omega)L-2\Delta\omega R/\omega_0}
$$
将上述分式上下同时乘以$-j$,并且同时除以$(\omega_0+\Delta\omega)L$之后,得到下面的表达式,
$$
Z(\omega_0+\Delta\omega)\approx\frac{R}{1+j\frac{2\Delta\omega R/\omega_0}{(\omega_0+\Delta\omega)L}}
$$
其中我们定义$Q=\frac{R}{\omega L}$为品质因数,在我们的这个问题中,品质因数定义为$Q_L=\frac{R}{(\omega_0+\Delta\omega)L}$,因此,根据这一个等式,上面的阻抗表达式可以进一步表示为,
$$
Z(\omega_0+\Delta\omega)\approx\frac{R}{1+j2Q_L\Delta\omega/\omega_0}
$$
需要注意的是,上述表达式仅仅在$\omega_0$振荡频率附近($\Delta\omega<<\omega_0$)才成立。
一般是计算等效输入噪声,噪声源作用在整个电路的输入上,振荡电路一般是一个正反馈环路,也就是如下图所示的电路框图结构,
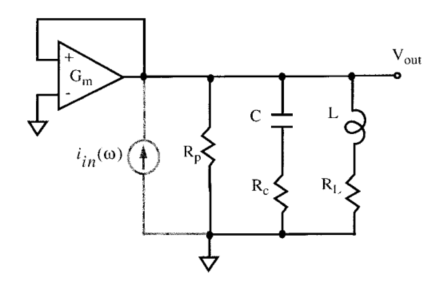
上面的噪声电流源相当于作用在这个正反馈环路上,因此传输函数可以用下面的表达式进行表达,
$$
H(\Delta\omega)=\frac{v_{out}}{i_{in}}
$$

