写在前面
最近在做项目时,遇到了需要使用传输线理论进行解释的电路,于是最近对传输线理论有了一个新的认识,并且,理论与实践相结合得到了一个比较容易理解的认识。
传输线理论
当传输线的长度和波长差不多时,直观上读者就可以想象,在传输线上各点的相位肯定不一样,这时就会导致传输线上各点的电压不同,这就是传输线效应。一般来讲,当传输线的长度大于波长的$1/10$时,就需要考虑这种效应了。
传输线方程
基本的传输线模型如下图所示,
传输线本质上是一个拥有返回路径的长度为$z$导线,然后为了方便分析,将传输线分割成长度为$\Delta z$的导线,定义电阻、电感、电导、电容的单位长度密度为如下,
$R’=\rho/A[\Omega/m]$:单位长度下的电阻大小;
$L’=\mu[H/m]$:单位长度上的电感大小;
$G’=1/R’[S/m]$:单位长度上的导纳大小;
$C’=\epsilon A/d[F/m]$:单位长度上的电容大小;
一般来说,在集成电路里面,电感的大小为$1nH/mm$,电容的大小为$1fF/\mu m$。需要注意的是,电感的长度密度大小是与真空磁导率$\mu_0=4\pi\times10^{-7}\approx1.25e-6$直接相关的,大概是$1.25nH/mm$,这个值与我们之前给的经验值基本一致,这里需要解释一下为什么使用真空磁导率计算的电感密度结果就与经验值差不多,这是因为铝和铜这两种导线材质的相对磁导率基本接近1,所以不需要对磁导率进行调整。
将传输线进行微分后,得到如下的微元,
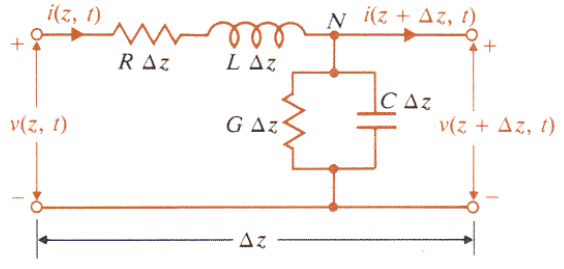
写出上图中的KVL方程:
$$
v(z,t)=R\Delta zi(z,t)+L\Delta z\frac{di(z,t)}{dt}+v(z+\Delta z,t)
$$
写出上图中的KCL方程:
$$
i(z,t)=G\Delta zv(z+\Delta z,t)+C\Delta z\frac{dv(z+\Delta z,t)}{dt}+i(z+\Delta z,t)
$$
如果$\Delta z\rightarrow0$,那么上述的两个表达式可以化为如下的互耦表达式,
$$
-\frac{\partial v(z,t)}{\partial z}=R(i,t)+L\frac{\partial i(z,t)}{\partial t}
$$
$$
-\frac{\partial i(z,t)}{\partial z}=Gv(z,t)+C\frac{\partial v(z,t)}{\partial t}
$$
对于正弦波输入的电压和电流而言,可以使用如下的Phasor(相量)形式,
$$
v(z,t)=Re{V(z)e^{j\omega t}}
$$
$$
i(z,t)=Re{I(z)e^{j\omega t}}
$$
上述两个方程和的解如下,
$$
V(z)=V^+(z)+V^-(z)=V_0^+e^{-\gamma z}+V_0^-e^{\gamma z}
$$
$$
I(z)=I^+(z)+I^-(z)=I_0^+e^{-\gamma z}+I_0^-e^{\gamma z}
$$
上述方程将波分为了两个方向传播的过程,一个是正向的传播,还有一个是负向的传播,该方程描述了电压在传输线上的分布,其中$\gamma$是一个无量纲的数值,称为传输常数(Transmission Constant),主要描述了电压在传输线上的分布特征。读者可以想象,$\gamma$是一个类似于$e^{\omega t}$中的$\omega$,这个值主要描述了电压的相位在时间轴上的变化速度,$\omega$越大,在时间轴上,电压相位变化速度越快;同样的,在距离x轴上,$\gamma$越大,电压相位在相同距离上变化得越多。
传输常数$\gamma$的表达式如下所示,
$$
\gamma=\alpha+j\beta=\sqrt{(R+j\omega L)(G+j\omega C)}
$$
如果这里的衰减系数为0,那么$\gamma=j\beta$,该传输函数的量纲为$[rad/m]$。
这里还给出了特征阻抗的定义,
$$
Z_0=\frac{V_0^+}{I_0^+}=-\frac{V_0^-}{I_0^-}=\frac{R+j\omega L}{\gamma}=\sqrt{\frac{R+j\omega L}{G+j\omega C}}
$$
注意到这里的量纲为$[\Omega/m]$。
特征阻抗$Z_0$和传输函数$\gamma$是传输线两个最重要的参数,值得注意的是,这两个参数与传输线的长度无关,只与传输线上的($RLGC$)有关。
无损传输线案例分析
对于无损传输线来说,电阻$R$以及电导$G$的贡献均为零,因此,对于传输常数来说,只会在长度上产生相位的变化,并不会产生衰减。在这一层面上,传输函数的意义非常明确,传输函数代表了一定长度上,电压相位的变化,因此,如果要知道信号在传输线中的波长,只需要知道相位变化$2\pi$时,走了多少长度即可,因此波长由下式表达,
$$
\lambda=\frac{2\pi}{\gamma}=\frac{2\pi}{\beta}=\frac{1}{f\sqrt{LC}}
$$
对于一个10GHz的信号来说,根据先前我们给定的如下经验参数,
$$
L=1nH/mm
$$
$$
C=1fF/\mu m
$$
可以计算得到10GHz的信号在芯片传输线中的波长为如下,
$$
\lambda=\frac{1}{f\sqrt{LC}}=\frac{1\mu m}{10G\sqrt{1pH\times 1fF}}=3.16mm
$$
因此,对于10GHz左右的信号来说,300um以上的线就必须要考虑传输线效应了。
在考虑特征阻抗,如果传输线时无耗传输线,那么,特征阻抗的表达式如下所示,
$$
Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}=\sqrt{\frac{L}{C}}
$$
如果使用我们的经验参数计算特征阻抗,得到下面的数值,
$$
Z_0=\sqrt{\frac{L}{C}}=\sqrt{\frac{1pH/\mu m}{1fF/\mu m}}=32\Omega
$$
Terminated的传输线的反射
反射系数$\Gamma$描述了反射波与入射波的比例,反射系数$/Gamma$的表达式如下,
$$
\Gamma=\frac{V_0^-}{V_0^+}=\frac{Z_L-Z_0}{Z_L+Z_0}
$$
上述表达式很容易记忆,$Z_0$表示传输线的特征阻抗,$Z_L$表示传输线驱动的负载。当传输线驱动的负载为开路,也就是无穷大时,传输线应该将所有信号全部反射回去,也就是反射系数为1,这样就把表达式分子上的符号记住了。
接下去给出传输线反射相关的内容的一个计算实例,假设一个800um的传输线,16GHzCMOS时钟,驱动一个负载为$200fF$的电容,计算其在输入位置是否会因为反射而产生过压现象?
首先根据先前的经验公式,得到传输线的特征阻抗为,
$$
Z_0=\sqrt{\frac{L}{C}}=\sqrt{\frac{1pH/\mu m}{1fF/\mu m}}=32\Omega
$$
接下去计算反射系数$\Gamma$,
$$
\Gamma=\frac{\frac{1}{j\omega C}-32}{\frac{1}{j\omega C}+32}=\frac{1-32j\omega C}{1+32j\omega C}=\frac{1-0.1024j}{1+0.1024j}\approx1\angle-11.69\degree
$$
可以发现,该反射波在原先输入波的基础上,滞后了$11.69\degree$,幅度基本不变,如果反射波和入射波进行叠加之后,产生的新的波形的幅度可以看到是变为原先正常波形的接近两倍。

