写在前面
二阶系统一般有两个极点组成,这两个极点的距离的关系决定了二阶系统的稳定性,本质上这种分析方法是在求解偏微分方程的解。注意,这里所说的二阶系统的方程都是说的是闭环系统。
二阶系统的基本概念
先给出一个二阶系统的拉普拉斯方程。
$$
Sys(s)=\frac{1}{s^2+2\zeta \omega_ns+\omega_n^2}
$$
其中的$\zeta$是阻尼系数,$\omega_n$是自然频率。
接下去我们给出由阻尼系数和自然频率给出的极点位置的表达式。
$$
P = -\zeta \omega_n\pm j\omega_n\sqrt{1-\zeta^2}
$$
我们可以看出极点的辐角,由下面的表达式表达,
$$
\theta=\pm arctan\frac{\sqrt{1-\zeta^2}}{\zeta}
$$
求解相位裕度
这里读者需要注意,直接从我们之前的闭环传输函数推导出相位裕度是不可行的,因为相位裕度本身就是在开环传输函数上求解的,因此,我们需要知道开环传输函数与我们的闭环传输函数之间的关系。
假设下面的开环传输函数,
$$
A_{OL}=\frac{A_o}{(1+s/s_1)(1+s/s_2)}=\frac{A_o}{1+(1/s_1+1/s_2)s+s^2/(s_1s_2)}
$$
通常来说,我们的闭环传输函数的反馈系数$\beta = 1$,因此,求得下面的闭环传输函数。
$$
A_{CL}=\frac{A_{OL}}{1+A_{OL}\beta}=\frac{A_o}{1+(1/s_1+1/s_2)s+s^2/(s_1s_2)+A_o}
$$
将上式化简之后我们可以获得如下的表达式,
$$
A_{CL}=\frac{1}{1+\frac{s}{s_1A_o}+\frac{s^2}{s_1A_os_2}}
$$
可以看到,这里做了一些化简,并且注意到,假设$s_1$是主极点,有,$s_1A_o=GBW$,再重新写一下上式,我们可以获得如下的信息,
$$
A_{CL}=\frac{1}{1+\frac{s}{GBW}+\frac{s^2}{GBWs_2}}
$$
再根据我们先前推导的二阶系统的表达式,我们可以知道如下信息,
$$
PM=\frac{\pi}{2}-arctan\frac{GBW}{s_2}
$$
$$
\omega_n=\sqrt{GBWs_2}
$$
$$
2\zeta \omega_n=s_2
$$
$$
\zeta=\frac{1}{2}\sqrt{\frac{s_2}{GBW}}
$$
由上面的式子我们可以直接由系统的参数写出系统的阻尼系数、振荡频率等参数。简单来说,阻尼系数由非主极点和GBW的比例决定,比例越大,非主极点离GBW距离越远,阻尼系数越大。一般情况下,阻尼系数设置为$\frac{1}{\sqrt{2}}$合适,这时候,非主极点为GBW的两倍,相位裕度为63°左右。
品质因素$Q$的定义
我们再研究一下Q的定义,在滤波器中Q的定义为幅度最大的频率$\omega_o$与滤波器的3dB带宽的频率$\Delta\omega$的比值,由下面的式子表达。
$$
Q’=\frac{\omega_o}{\Delta\omega}=\frac{\omega_n}{\zeta\omega_n}=\frac{1}{\zeta}
$$
实际的Q需要在此值上除以一个2,这里还没有一个很好的解释,如下面的式子所示,
$$
Q=\frac{1}{2\zeta}
$$
如果阻尼系数$0<\zeta<1$,这也是通常我们研究的情形,在这种情形下,振荡频率会从原先的0阻尼振荡频率$\omega_r=\omega_n$,修正为$\omega_r=\omega_n\sqrt{1-\zeta^2}$。这里需要特别说明一下表达式$\sqrt{1-\zeta^2}$本身也是有一定物理意义的。
$\sqrt{1-\zeta^2}$的物理意义
该量在二阶系统的很多数学特征中有所体现,体现为一个修正量,这个修正量与阻尼系数成反比,阻尼系数越大,该修正量越小,修正得越多,阻尼系数越小,该修正量越接近于1,越趋近于不修正;并且,该修正量在阻尼系数大得时候,变化得更显著。因此,总结一下就是,修正量主要对阻尼系数大的情形进行修正,会将原先的量修正小。
频率响应的最大值
如果阻尼系数$0<\zeta<1$,那么,频率响应在谐振频率$\omega_r=\omega_n\sqrt{1-\zeta^2}$处取得最大值,将,上述表达式代入二阶系统的频率响应中,得到最大的幅频响应值,这个值也是peaking的大小,表达式如下所示,
$$
P_r=\frac{1}{2\zeta\sqrt{1-\zeta^2}}=\frac{Q}{\sqrt{1-\zeta^2}}
$$
可以看到,Q一定程度上代表了Peaking的高度,只不过被修正了,阻尼系数越大,修正得越多,阻尼系数越小,修正得越少。所以在一些小阻尼系数得系统里面,可以直接使用Q估计Peaking的高度。
二阶系统的瞬态响应时域表达式
先给出二阶系统的瞬态响应时域表达式:
$$
y(t)=1-e^{-\zeta\omega_n t}(cos(\omega_r t)+\frac{\zeta}{\sqrt{1-\zeta^2}}sin(\omega_r t))
$$
其中,$\omega_r$指的是阻尼系数修正后的振荡频率,如下所示,
$$
\omega_r=\omega_n\sqrt{1-\zeta^2}
$$
其瞬态响应的最大值出现在$\frac{\pi}{\omega_r}$处,把这个值代入到时域的瞬态表达式中,我们可以得到如下的瞬态响应最大值,
$$
M_p=1+e^{\frac{-\pi\zeta}{\sqrt{1-\zeta^2}}}
$$
将上述表达式绘制成图像,可以得到如下结果,
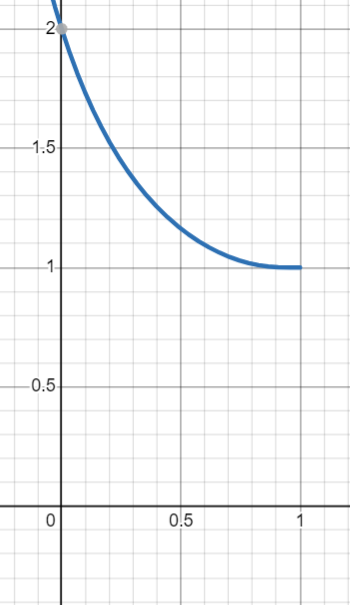
观察图片可以发现,当阻尼系数为零时,过冲最大,当阻尼系数为1时,没有过冲。
案例分析
分析一个闭环放大器,该放大器的开环响应存在主极点@10kHz,非主极点@2MHz,该放大器的开环增益为40dB,反馈系数为1,分析该二阶系统的各项参数。
先给出该放大器的s域开环系统传递函数:
$$
A_{OL}=\frac{100}{(s/1e4+1)(s/2e6+1)}=\frac{100}{s^2/2e10+s/1e4+1}
$$
再计算闭环系统的传递函数:
$$
A_{CL}=\frac{100}{s^2/2e10+s/1e4+100}=\frac{2e12}{s^2+2e6s+2e12}
$$
接下去可以求解出该表达式的自然频率$\omega_n$,如下所示,
$$
\omega_n=\sqrt{2e12}\approx1.414MHz
$$
接下去求解系统的阻尼系数$\zeta$,如下所示,
$$
2\zeta\omega_n=2e6
$$
$$
\zeta=\frac{2e6}{2\omega_n}=\frac{1}{\sqrt{2}}
$$
这里还需要说明,当阻尼系数为0.707时,该传输函数称为一种特殊的滤波器:Butterworth Filter。这里简单介绍一下Butterworth滤波器,这种滤波器在带内完全平坦,这里需要说明的是,这里说的平坦是指滤波器频率响应,而不是瞬态响应,要记住,Butterworth滤波器的瞬态响应根据先前的计算,是存在一定的过冲的。Butterworth滤波器的频率响应具有一下的特点:
- 在通带内的幅度响应的平坦的;
- 频率响应从通带到禁带的变化是单调的,即不存在任何的上下波动;
- 禁带内的滚降是平滑的,并且随着滤波器阶数的上升而上升。
值得注意的是,Butterworth由于其通带内平坦的特性而被广泛应用,但是其从通带到禁带的过渡部分不像切比雪夫滤波器和椭圆滤波器那样迅速滚降,即滚降速率比较慢。
计算品质因素Q的值,根据之前的表达式$Q=\frac{1}{2\zeta}$,Q的表达式由下式表达,
$$
Q=\frac{1}{2\zeta}=\frac{1}{\sqrt{2}}=0.707
$$
有了Q之后,我们就可以计算修正后的Q,这个值代表了幅频响应中的Peaking高度$P_r$
$P_r=\frac{Q}{\sqrt{1-\zeta^2}}=\frac{1/\sqrt{2}}{1/\sqrt{2}}=1$
这也论证了我们之前说这是一个Butterworth滤波器的结论。接下去再计算时域中的过冲$M_p$,由下式表达
$$
M_p=e^{\frac{-\pi\zeta}{\sqrt{1-\zeta^2}}}=e^{-\pi}\approx0.04
$$
可以看到瞬态响应中是由一定的过冲的,过冲的比例$%OS$为$4%$基本可以忽略不计。

