写在前面
最近感觉对一些电路的理解还不够深入,比如说Bandgap的噪声和PSRR计算,Bandgap的失调计算,这些内容我都没有思考过,每次想起都让我觉得心里不适。因此,我下定决定,再度回到本源,从基础开始,再学习一遍模拟IC设计,学习得到的经验都记录在我的博客里,形成一套阅读笔记,以供之后查看。
简介
作者主要想要表达的意思是,模拟IC设计涉及到很多模型的应用,如果要用好这些模型,设计者需要对模型的来源和近似程度有个比较透彻的了解才行,因此,估计本章都在进行模型的推导和解释工作。作者说,本章的重点主要放在半导体器件行为模型上的一些基本概念,以及如何通过等效电路来建模这些行为。
PN结的耗尽区
反偏PN结广泛存在于IC设计中,并且产生了许多寄生电容,这些寄生电容大小与反偏电压的大小相关,除了产生寄生电容,PN结还对有源器件的其他特性产生影响,例如,
- 击穿电压
- 输出电阻
- jfet的工作特性
总之,这个非常重要,所以在这里重点讨论了这个概念。
扩散运动产生真空电荷区
考虑上图$(a)$中的一个PN结,这个结的P区掺杂浓度定义为$N_A$ $atoms/cm^3$,N区掺杂浓度定义为$N_D$ $atoms/cm^3$。因为P区和N区的载流子浓度不一样,所以会产生扩散效应,P区的空穴扩散到N区,N区的电子扩散到P区,造成P区聚集了带负电的离子,N区形成了带正电的离子。由于可以移动的电子和空穴都因为扩散运动而消失了,只留下了不可移动的离子,并且P区的离子带负电,N区的离子带正电,造成在结附近的区域产生了大量的空间电荷并且导致了很强的电场。这个区域称耗尽区(Depletion Region,因为可以自由移动的电荷被耗尽了),或者被称为空间电荷区(Space-Charge Region)。值得注意的是,作者假设了耗尽区的边界和上图$(b)$中的边界一样,会有浓度的突变,边界非常陡峭,作者说这在大多数情形下都是一个非常好的近似。
内建电势(电压)
想象一个问题,将可乐和水倒在一起,可乐会扩散到水中,水会扩散到可乐中,最终的结果是液体中的可乐浓度处处一致。那么,PN结中的扩散也会导致最终PN半导体变得处处一致吗?
这两种情况产生不一样的结果的原因在于,可乐中的分子扩散到水中,并不会产生后果,而N型半导体中的电子扩散到P型半导体中,会导致P型半导体不再是电中性,在电荷层面不再平衡,虽然在浓度层面PN结有走向平衡的趋势,但是代价却是电荷层面的不平衡,这种不平衡会产生一个内建的电场,从而产生电势差。最终,浓度的不平衡和电荷的不平衡互相对抗,达到一种新的平衡。
如果PN结两侧外加电势差为0电荷的不平衡由下面的电势差表达式表达,
$$
\psi_0=V_Tln\frac{N_AN_D}{n_i^2}
$$
其中,热电压$V_T=26mV@300K$,$n_i$是本征半导体的载流子浓度,表示了在一个纯净的半导体中,例如,Si晶体中,电子和空穴的浓度,$n_i\approx1.5\times 10^{10}cm^{-3}$。
计算N型与P型半导体耗尽层的宽度
电荷守恒
由于电荷守恒,两个结的横截面积是一样的,如果耗尽层在浓度为$N_A$ $cm^{-3}$的P型半导体中的宽度为$W_1$,耗尽层在浓度为$N_D$ $cm^{-3}$的N型半导体中的宽度为$W_2$,所以可以推导出如下的表达式,
$$
W_1N_A=W_2N_D
$$
简单来说,浓度小的宽度大,浓度大的宽度小,这样两侧的空间电荷区的电荷总量才能保持数量一致符号相反,保持整体呈现电中性。
Poisson Equation
接下来要给出一维层面的Poisson公式,先给出通常的Poisson公式,
$$
\nabla^2\psi=f
$$
其中,需要解释的是拉普拉斯算子$\nabla^2$,根据定义来说,该算子施加于Scalar Field(标量)后,可以给出Scalar Field在某点处的曲率。简单来说,该算子就是一个峰(局部最大值)和谷(局部最小值)的检测器。根据上述描述,Poisson公式想要说的是,某标量场出现峰和谷的条件是,有一个外界的影响元$f$,换句话说,如果没有影响元$f$的存在,那么,该标量场就不会存在峰或谷值,体现为一个斜坡或者平台。
在静电学中,Poisson公式表示为如下,
$$
\nabla^2\psi=-\frac{\rho}{\varepsilon_0}
$$
其中,影响元$f$为电子,但是,由于电子可能处在不同的介质中,不同介质中,电子产生电场的能力是不一样的,这里使用Permittivity(介电常数)来衡量这一特性,介电常数越大,电子产生电场的能力越弱,介电常数越小,电子产生电场的能力越弱,下面给出一些常见的介质的介电常数。
| Material | Relative Permittivity ($\varepsilon_r$) |
|---|---|
| Vacuum | 1 (by definition) |
| Air | 1.0006 |
| Distilled Water | ~80 (at 20°C) |
| Quartz | ~3.8 |
| Common Window Glass | ~4 - 7 |
| Pyrex | ~4.5 |
| Teflon (PTFE) | ~2.1 |
| Rubber | ~2 - 7 (depending on type) |
| Mica | ~5 - 8 |
| Polyethylene | ~2.3 |
| Barium Titanate | ~1200 - 5000 (variable) |
| Crystalline Silicon | ~11.7 |
| Silicon Dioxide (SiO2) | ~3.9 |
真空中的介电常数为$8.86fF/mm$,这个参数比较好记,大概量级就是”一毫米十飞法”。
将Poisson公式写成一维的形式,如下所示,
$$
\frac{d^2V}{dx^2}=-\frac{\rho}{\varepsilon}=\frac{qN_A}{\varepsilon}
$$
这里由于在描述P型半导体(Acceptor)的电荷密度,在P型中的真空电荷区的电荷带负电,因此,抵消了原先的负号。
导出电场
对上式积分有,如下表达式,
$$
\frac{dV}{dx}=\frac{qN_A}{\varepsilon}x+C_1
$$
由于电势差增长方向(导数为正方向)与电流方向(正电荷受力移动方向)相反,因此,电场表达如下,
$$
E=-\frac{dV}{dx}=-(\frac{qN_A}{\varepsilon}x+C_1)
$$
使用边界条件$E=0$ @ $x=-W_1$,得到下面的表达式,
$$
E=-\frac{dV}{dx}=-(\frac{qN_A}{\varepsilon}x+\frac{qN_A}{\varepsilon}W_1)
$$
导出电势
对上式继续做积分,由下面的表达式,
$$
V=\frac{qN_A}{2\varepsilon}x^2+\frac{qN_A}{\varepsilon}W_1x+C_2
$$
假设$V=0$ @ $x=-W_1$的边界条件,那么可以给出下面的表达式,
$$
V=\frac{qN_A}{2\varepsilon}x^2+\frac{qN_A}{\varepsilon}W_1x+\frac{qN_A}{2\varepsilon}W_1^2
$$
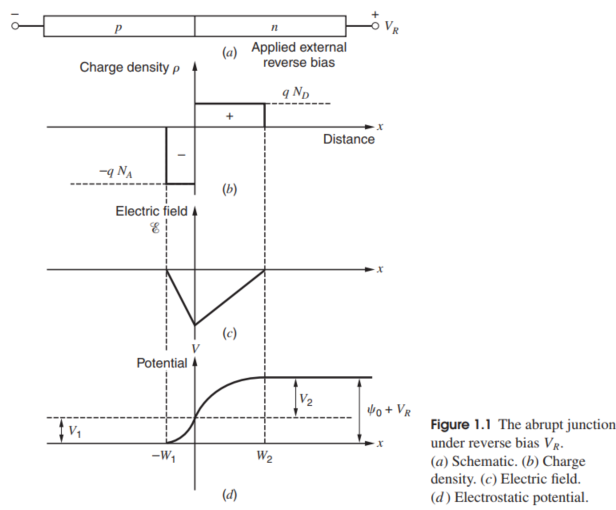
计算结的电势差$\psi_0+V_R$
先计算从结的中间$x=0$到P型半导体空间电荷区的边界$x=-W_1$的电势差$V_1$,如下所示,
$$
V(0)-V(-W_1)=V(0)=\frac{qN_A}{2\varepsilon}W_1^2
$$
根据对偶性,我们可以马上写出从N区空间电荷区$x=W_2$到结的中间$x=0$的电势差$V_2$
$$
V_2=\frac{qN_D}{2\varepsilon}W_2^2
$$
马上我们可以写出总的结电压差(内建+外加)的表达式,
$$
\psi_0+V_R=\frac{q}{2\epsilon}(N_AW_1^2+N_DW_2^2)
$$
接下去根据关系:$W_1N_A=W_2N_D$,马上就可以分别给出$W_1$和$W_2$的表达式,如下所示,
$$
W_1=[\frac{2\varepsilon(\psi_0+V_R)}{qN_A(1+\frac{N_A}{N_D})}]^{1/2}
$$
$$
W_2=[\frac{2\varepsilon(\psi_0+V_R)}{qN_D(1+\frac{N_D}{N_A})}]^{1/2}
$$
上面两个表达式中,我们可以发现耗尽区宽度与杂质浓度成反比,并且与内建和外加反向电压之和成正比,耗尽区总是在轻掺杂的一侧更宽。
耗尽区电容
我们先给出结电容的微分表达式,如下所示,
$$
C_j=\frac{dQ}{dV_R}=\frac{dQ}{dW_1}\frac{dW_1}{dV_R}
$$
空间电荷区的电荷大小与宽度的关系如下所示,
$$
dQ=qN_AAdW_1
$$
其中,$A$代表了横截面积,$AdW_1$直接代表了体积微元。进一步计算得到,结电容的表达式如下所示,
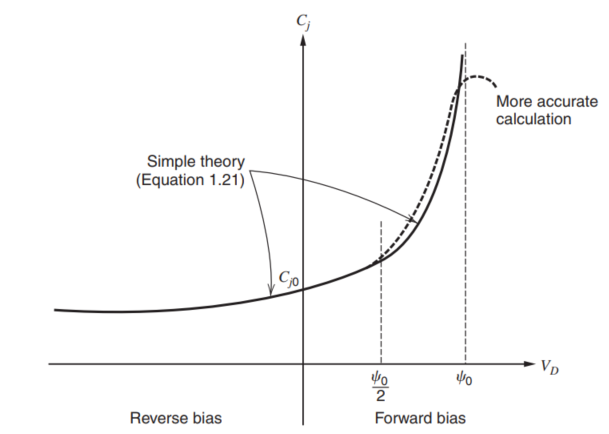
$$
C_j=\frac{C_{j0}}{\sqrt{1-\frac{V_D}{\psi_0}}}
$$
其中,$C_{j0}$表示了当$V_D=0$时的结电容,该曲线对应了下图中的1.21,但是实际上,该表达式在推导时,假设了P和N半导体都是均匀掺杂的,但实际上,掺杂浓度是有一个梯度的,因此,经过计算后,原先分母的平方根(1/2次方)应变为立方根(1/3次方)。并且,这里也假设了当V_D趋近于$\psi_0$时,电容会趋近于无穷大,这也是不合理的,实际的曲线应该为下方的虚线所示。
结的击穿
这部分内容感觉用不太到,等用到了之后再读。
双极性晶体管的大信号行为
大信号行为包括:
- 总电压、总电流大小;
- 击穿电压上限;
- 二阶效应(电流增益随着集电极电流 & Early电压变化)
Large Signal Models in Forward Active Region
典型的三极管的结构如下所示,
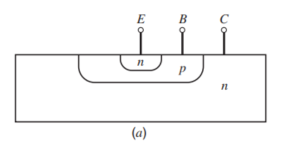
要注意到,这种结构的三极管的掺杂浓度往往不是一个常量,而是一个有梯度的量,我们先从均匀掺杂浓度的管子开始分析,而后这里得到的结论有一些也可以在非均匀的管子里面应用。下面的图片就表示了一个均匀掺杂的三极管的示意图。
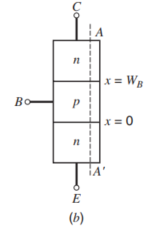
基区中的载流子浓度计算
如上图所示,在AA’的横截面上取出一个掺杂浓度的样本,可以得到如下所示的载流子浓度示意图。
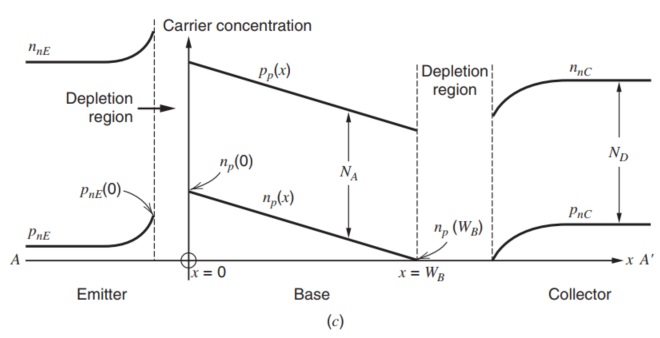
空穴浓度用p表示,电子浓度用n表示,其中,下标的n和p表示所处的半导体的类型;E和C的下标分别代表发射极和集电极。上图中表示的载流子浓度是在管子偏置在Forward Active Region中的载流子浓度分布,在这种情况下,Base和Emitter的PN结正向导通,而Base和Collector的PN结是反向偏置的。
我们先给出由Fermi-Dirac分布函数通过Boltzmann Approximation得到的下面的关于电子浓度分布在$x=0$和$x=W_B$处的表达式,
$$
n_p(0)=n_{po}exp(\frac{V_{BE}}{V_T})
$$
$$
n_p(W_B)=n_{po}exp(\frac{V_{BC}}{V_T})\approx0
$$
其中,$n_{po}$表示了在P型半导体中,在无任何电压激励状态下,电子的浓度。可以看到,如果在PN结的P一端施加更高的电压,也就是$V_{BE}$更大,在P型半导体一端的耗尽层边缘的电子浓度会急剧上升,Fermi能级会大大上升,因为Fermi能级指的是电子的50%出现概率的能级点。随着电压上升,电子留在P中的概率大大上升,自然Fermi能级就会上升。
这里讨论几个我产生的疑问:
为什么这个表达式中会产生指数?
因为这里是在说P型半导体中的电子,属于少子浓度,少子浓度一般都是在Fermi-Dirac分布的尾端,而Fermi-Dirac分布的尾端近似指数分布,因此,指数分布就是这么来的。
为什么这个表达式中是$V_{BE}/V_T$?
首先,我们要弄清楚,上面这个指数表达式是Fermi-Dirac分布的一种近似,其原先的含义是,给出某个粒子的能量,马上可以通过Fermi-Dirac分布给出该能量下,该粒子出现的概率。简单来说,能量越低,找到该粒子的概率越大;能量越高,找到该粒子的概率就越小。这时,怎么判断能量的高低呢?物理学家使用$kT$这一量来衡量能量的大小,这个量的含义是,粒子的热能的数学期望,是一个统计学的量。如果,能量差超过均值很多,那么,找到这个粒子的概率就大大降低;反之,如果能量差小于均值很多,找到这个粒子的概率就大大升高。这个概念直观上来说,可以用一群孩子在书架上拿书的情形来解释,假设这些孩子都是一样高的,但是孩子跳得不一样高,但孩子跳的高度均值为$kT$,那么,书架上的书如果超过$kT$很多,自然被孩子拿去的概率就大大降低,如果小于$kT$很多,被孩子拿去的概率就很大了。这里之所以是$V_{BE}/V_T$而不是$V_{EB}/V_T$的原因在于,衡量的量是P型半导体基极的电子的概率,如果B上施加正向的电压,会使得基区的费米能级上升,自然,n区少数载流子(自由电子)的浓度就上升了。
在上图中,还有一个值得观察的点是,在BE的耗尽区界面和BC的耗尽区界面之间,是线性链接的,这是因为什么呢?这里,作者直接给出了文字的解释:如果在基区的电子和空穴的重新结合的量很小,那么中间的分布就可以看作是线性变化的。这里可以直观地用水来理解,想象一个水渠,有AB两端,水从A端被放入,从B端被放出,水面的高度被认为是载流子的浓度,这里,我们认为是少子电子的浓度,$n_p(x,t)$。如果,输入恒定,且输出恒定,最终水渠内的水的高度会达到稳定,不再跟随时间发生变化,即,
$$
\frac{\partial n_p(x,t)}{\partial t}
$$
少子与多子的重新结合(Recombination),可以被认为是水渠的中间挖了一些小洞,如果小洞流出的水相对于水流量来说很少,那么,可以认为小洞不存在,由于输出端流出水流,所以输出端的水面位置自然会低一些,输入端的睡眠位置自然会高一些,之间自然是线性变化的,也就是下面的表达式,
$$
\frac{\partial^2 n_p(x,t)}{\partial x^2}=0
$$
对于基区来说,耗尽区外的部分仍然为电中性,所以,需要保证多出来的一份自由电子必须要有一份多出来的空穴,本身的自由空穴与一开始的掺杂浓度是一样的,所以要有下面的式子成立,
$$
N_A+n_p(x)=p_p(x)
$$
由于之前假设了基区掺杂浓度处处相等,所以,这边也可以认为基区的空穴浓度$p_p(x)$也是一个在x(位置)上线性的量。
集电极电流
接下去来探讨通过扩散作用的电子到了BC的界面上该如何运动的问题,想象下面的一个直观的粒子,在夏日的海滩上,海里有很多人,沙滩的一边代表基极,人源源不断地从沙滩进入到大海,代表着基极的扩散运动,这时,大海里的人少,沙滩上的人多,形成了一个梯度,这时,大海里突然产生了离岸流,将在海里的人拉到了深海里,这就像是基极和集电极之间的电场作用,将人(电子)拉到海洋里(集电极),形成了电流。作者使用了扫进集电极的术语,说明了人(电子)在对抗离岸流(电场)时,力量很小,只要被卷入了海洋(集电极),就很难再回来了。
同样地,在晶体管里面,也是一样的概念,电子由于基极的浓度差,形成了一个梯度,导致电子往低浓度的方向扩散,当电子移动到BC的界面的时候,电场非常强,一下子把扩散到这个地方的电子吸入了集电极,产生了很强的电流。
我们接下去用数学的方式来描述一下这个过程,如下所示,
$$
J_n=qD_n\frac{dn_p(x)}{dx}
$$
上式描述了扩散电流密度,其中,$D_n$表示了电子的扩散常数,由于电子的浓度在距离上的斜率固定,所以可以用下式表达,
$$
J_n=qD_n\frac{n_p(0)-n_p(W_B)}{0-W_B}=-qD_n\frac{n_p(0)}{W_B}
$$
上式乘以面积就是集电极电流了,如下所示,
$$
I_C=qAD_n\frac{n_p(0)}{W_B}
$$
将BE界面的少子浓度$n_p(0)$代入到上面的表达式后,得到如下的表达式,
$$
I_C=\frac{qAD_nn_{po}}{W_B}exp\frac{V_{BE}}{V_T}=I_Sexp\frac{V_{BE}}{V_T}
$$
其中,$I_S=\frac{qAD_nn_{po}}{W_B}$,一般这个数值的量级为$10^{-14}$ ~ $10^{-16}A$之间,属于$fA$量级,相当小。
基极电流
基极电流也是一个非常重要的量,作者给出了基极电流的两个分量,一个是空穴和电子的重新结合(Recombination),和我们前文说的水渠的案例可以结合起来看,这个水渠中的流水代表了电子的流动,水渠中间挖去一些洞,水流会流走一些,就代表了空穴和电子的重新结合(Recombination),可以由此来直观地理解这个机制。
下面使用数学来描述这个过程,定义$I_{B1}$为重新结合的电子和空穴形成的电流,该电流与基区的少子电子$Q_e$成正比,该量表示如下,
$$
Q_e=q\int_{0}^{W_B}n_p(x)Adx=\frac{1}{2}qAW_Bn_p(0)
$$
定义$\tau_b$为基区少子的平均生存时间,那么,该时间内,基区所有少子都会被重新结合,所以,该电流表示如下,
$$
I_{B1}=\frac{Q_e}{\tau_b}=\frac{1}{2}\frac{qAW_Bn_p(0)}{\tau_b}
$$
另一个主要部分的电流主要来自于空穴的扩散,造成了空穴从基极注入到了发射极,如下所示,注意,这一部分电流主导了基区电流,后面的集电极-基极电流的一章说了,这一部分电流占据了90%,而前面一部分由于基极电子与空穴的重结合造成的电流只占据了10%。
$$
I_{B2}=\frac{qAD_p}{L_p}p_{nE}(0)
$$
注意,该扩散运动的电子运动速率与单位长度上的浓度差$p_{nE}(0)/L_p$成正比。一般管子不希望有这一部分电流,因为这一部分电流过大会影响管子的性能和效率,管子一般不希望基极电流过大,这样,其电流放大倍数可以很大;另一方面,由于发射极重掺杂,所以,发射极一般是一个好的电子的发射端,而不是空穴的接收端。因此,从两个层面讲,该电流都不会太大。
$\beta$的定义
将上面表达的两个电流组合起来,得到了总的晶体管的电流如下所示,
$$
I_B=(\frac{1}{2}\frac{qAW_Bn_{po}}{\tau_b}+\frac{qAD_pp_{nEo}}{L_p})exp\frac{V_{BE}}{V_T}
$$
上述表达式对于不均匀基区掺杂的器件仍然适用,但基区电流存在二阶项,这对于低电流应用来说非常重要,将会在之后进行考虑。
利用集电极电流和基极电流的比例我们就可以得到电流系数$\beta$了,如下所示,
$$
\frac{I_C}{I_B}=\beta
$$
$\beta$被称作Forward Current Gain,前向电流增益,一般这个值在集成电路中NPN管大概在50-500之间,而PNP管略低,大概在10-100之间。
发射极电流 & $\alpha$的定义
由于基极电流和集电极电流都是流向基极的,所以,发射极电流为基极电流和集电极电流之和,如下所示,
$$
I_E=I_C+I_B=\frac{I_C}{\alpha}
$$
其中,
$$
\alpha=\frac{\beta}{1+\beta}
$$
$\alpha$的表达式也可以用下面的式子进行表达,
$$
\alpha=\alpha_T\gamma
$$
$$
\alpha_T=\frac{1}{1+\frac{W_B^2}{2\tau_bD_n}}
$$
$$
\gamma=\frac{1}{1+\frac{D_p}{D_n}\frac{W_B}{L_p}\frac{N_A}{N_D}}
$$
其中,$\gamma$称为发射极注入效率,该量为由发射极注入基极的电子电流与穿过BE界面的电子电流和空穴电流的总和,理想状况下,$\gamma=1$,通过使得发射极的掺杂浓度($N_D$)远远大于基极的掺杂浓度($N_A$),并且基极的宽度($W_B$)非常小,在这样两个条件下,电流几乎都是正向从发射极注入到基极的电子电流,而反向的空穴电流非常小。
还有一个参数$\alpha_T$称为基极传输因数,主要描述的是基极到集电极载流子到达的比例,也就是衡量了有多少载流子从基极被注入到集电极。如果把$W_B$设计得足够小,那么我们就可以获得一个接近1的$\alpha_T$。
很显然,如果将基极做得足够薄,也就是说$W_B$足够小,再将发射极掺杂浓度做得足够高,以至于发射极和基极得掺杂比例足够大,那么,我们就可以设计出一个$\beta$很大的管子。以前初次上模电课时,老师曾经说过,基极非常薄,发射极重掺杂,这些概念当时也只是听听就过了,现在,终于明白这些改进是为了提高$\beta$的大小。
下面给出了NPN三极管的大信号模型
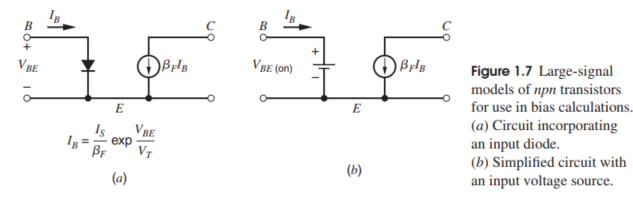
注意到左图中的电路很好解释,但是右图中,产生了一个新的变量$V_{BEon}$,这个变量的大小常在0.6-0.7V之间,这和我们的三极管的指数特性是对应上的,即电压的微小变化就会造成巨大的电流变化,所以这里电压基本不怎么变化。值得注意的是,这个量是一个与温度有关的量,与温度成反比,大概的变化为$-2mV/K$。
总结一下
我认为Forward Active Region下的大信号行为可以用海滩上的人来进行直观地说明。海滩上的人相当于基区中的少数载流子,在海岸上的人永远是最多的,这对应了BE界面上的少数载流子浓度是最大的,在BC界面上,由于集电极和基极电压反偏,造成了浓度为零。这两个界面之间的浓度分布是关于位置线性变小的,由于扩散运动,少子在高浓度区域BE界面上,要往低浓度区域BC界面扩散,如果这个过程中的电子空穴结合可以忽略,那么,电流就仅仅会因为扩散运动而产生,这个电流的大小取决于BE界面到BC界面的浓度变化速率,也就是单位长度上的浓度差值,由于BC界面上的浓度值近似为零,所以仅仅由BE界面上的浓度决定,这个浓度与VBE正偏电压成指数关系,这也就是指数关系的由来。到了BC界面上的少子在强电场的作用下(用人被离岸流卷走来理解),穿过BC界面到达了集电极,形成了集电极电流。沙滩上的人肯定都是从沙滩外的马路来的,如果沙滩外马路上的人足够多(发射极重掺杂),那么进入沙滩的人的数量也会足够多,从沙滩返回公路的人就会非常少。如果沙滩的宽度足够窄(基区宽度小,薄基区),那么由于沙滩上容纳的人数有限(没有空穴与电子的结合),在浓度差的作用下,全部都更快地进入了大海(更大的电流),被离岸流吸走,最终进入海洋。
因此,可以看到,指数特性的来源在于BE界面上的正偏电压造成了少数载流子的数量上升剧烈,从而通过扩散运动形成与浓度相关的电流。读大学第一次学模拟课程是在大二,到现在研三了,才弄懂三极管指数特性的来源,真是惭愧。
集电极电压对Forward Active Region中的大信号模型产生的影响
我们一只认为集电极电压并不会对集电极电流大小,因为根据我们之前推导的过程,集电极电流相当于在海里被离岸流带走的人,其量只取决于从沙滩到海的人的梯度,即从BE界面到BC界面的少数载流子的浓度变化率,即单位长度上的浓度差,因此,基区做得越薄,其产生的集电极电流就越大。下面来讨论集电极电压对集电极电流产生影响的一些情形。
除了Forward Active Region之外,还有Saturation Region($V_{CE}$接近0)和Breakdown Region($V_{CE}$很大)这两个区域,如果三极管工作在这两个区域,那么,集电极电压对集电极电流有非常大的影响;如果在这两个区域中间,集电极电流会随着$V_{CE}$的上升而缓慢上升。
看一下下面的图马上读者就可以定性地直观地理解了,$V_{CE}$变大,那么,$V_{BC}$反偏电压就会反偏得更多,BC界面上的耗尽区就会因为反偏电压增大而增大,挤压了基区的空间,造成了基区宽度较小,根据我们先前的分析,基区宽度变小,直接导致基区的浓度场的梯度变大,直接导致集电极电流增大。
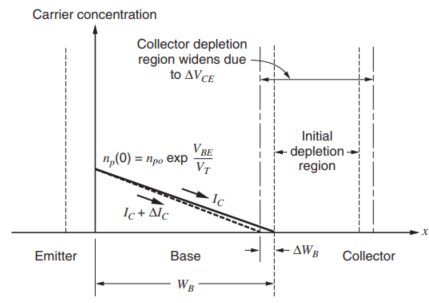
接下来需要定量分析一下,根据先前的集电极电流表达式,如下,
$$
I_C=\frac{qAD_nn_{po}}{W_B}exp\frac{V_{BE}}{V_T}
$$
对宽度$W_B$求导有如下表达式,
$$
\frac{\partial I_C}{\partial V_{CE}}=-\frac{qAD_nn_{po}}{W_B^2}exp\frac{V_{BE}}{V_T}\frac{\partial W_B}{\partial V_{CE}}=-\frac{I_C}{W_B}\frac{\partial W_B}{\partial V_{CE}}
$$
因为基区宽度随着$V_{CE}$的增大而减小,所以,上式的偏导为正,即,集电极电压增大,集电极电流也增大,与我们定性的分析一样。通过先前的耗尽区宽度与反偏电压关系的一节中的式子,可以进一步计算其斜率,其斜率是$V_{CE}$的函数,意味着他们之间存在一定的非线性,但这种非线性很弱,一般视作是一个恒定斜率的线性关系。
再来看上面表达式中的系数项,这一系数表明,$I_C$越大,$I_C$关于$V_{CE}$曲线的斜率越大,同时,由于IC中,基区的宽度都很薄,所以造成了$I_C$的作用被放大了。因此,可以得到如下的$V_{CE}-I_C$特性曲线,可以看到,相同$V_{CE}$的条件下,$I_C$越大,曲线的斜率越大。
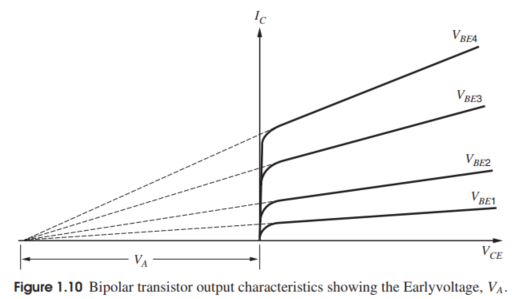
注意到,将曲线反向延长到横轴,会产生一个交点$V_A$,$V_A$的大小根据截距的定义,由下式表达,
$$
V_A=\frac{Y}{k}=\frac{I_C}{\frac{\partial I_C}{\partial V_{CE}}}=-W_B\frac{dV_{CE}}{dW_B}
$$
上述集电极电流跟随集电极电压发生变化的现象叫做Early Effect,$V_A$的典型值在15-100V之间。
在计算的时候,手算DC工作点的时候,一般不考虑Early效应,但是在小信号模型中,一般是考虑的。
Saturation and Inverse-Active Regions
通常在模拟电路中,器件一般不希望工作在Saturation Region,因为在这个区域里,管子的增益非常差,一般只会在数字中使用。
在Saturation的状态下,BE和BC的结都是正向导通的,在这种情形下,$V_{CE}$大概在0.05-0.3V之间,在$W_B$位置上的少子浓度如下所示,
$$
n_p(W_B)=n_{po}exp\frac{V_{BC}}{V_T}
$$
由于$V_{BC}$的值远大于零,这时,$n_p(W_B)$的值($W_B$处的少子浓度)就不可以被忽略了。根据先前的分析,集电极电流与基极的少子浓度斜率有关,自然与$[n_p(0)-n_p(W_B)]$成正比,换句话说,$n_p(W_B)$这一量直接影响到了集电极电流的大小,由于$V_C$电压直接影响到了$n_p(W_B)$的大小,因此,集电极节点呈现为一个低阻抗节点,即,微小的电压变化会产生巨大的电流变化。假设$V_{BE}$恒定不变,随着$V_{CE}$的减小,BC结界面上的结越来越正偏,$W_B$处的少子浓度越来越高,于是,产生了如下的器件特性,
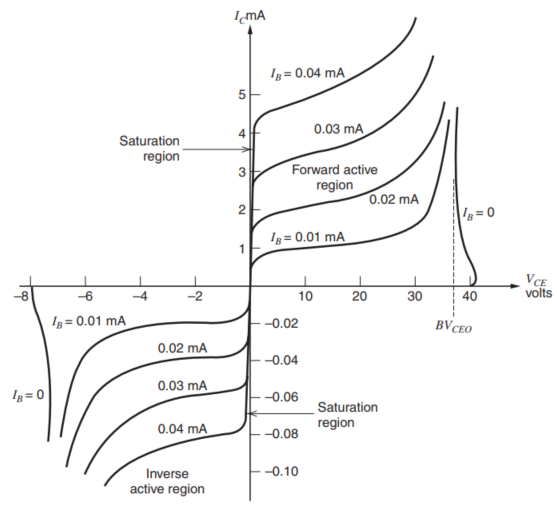
这时的电阻主要取决于集电极上的寄生电阻,通常在$20-500\Omega$之间。这时,处于饱和区三极管的器件模型由下面的模型描述,
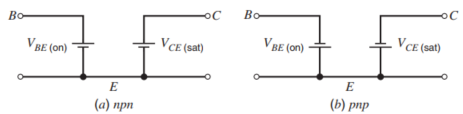
当双极型晶体管处于饱和区的时候,基区的电荷浓度显著高于Forward-Active Region,这时,由于电子空穴重新结合而产生的基极电流$I_B$会更大;另一方面,基极产生了新的电流分量,因为BC结的正向导通,$I_B$产生了BC结正向导通的电流的分量。这两个因素导致了双极型晶体管在同一集电极电流$I_C$的条件下,在Saturation Region状态下的基极电流会显著大于在Forward-Active Region状态下的基极电流。根据定义,对应的电流系数$\beta$也会显著低于处于Forward-Active Region状态下的晶体管。
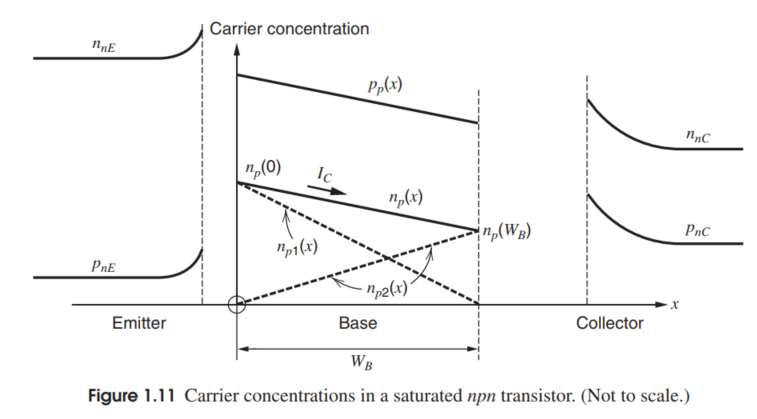
如上图所示,少子浓度可以看作是两条虚线浓度的叠加产生的,这样看待这个问题的条件是,基区电子和空穴的重结合(Recombination)非常小,这个条件前文我们说过如何直观地看待它。那么,由于$n_{p1}(x)$导致的发射极电流由下式表达,
$$
I_{EF}=-I_{ES}(exp(\frac{V_{BE}}{V_T})-1)
$$
$n_{p2}(x)$导致的集电极电流使用如下表达式进行表达,
$$
I_{CR}=-I_{CS}(exp\frac{V_{BC}}{V_T}-1)
$$
注意,根据之前的分析,只有一部分的发射极电流最终到达了集电极,比例为$\alpha_F$。因此,集电极电流由下面的式子表达,
$$
I_C=\alpha_FI_{EF}+I_{CR}
$$
通常来说,$\alpha_F$非常趋近于1,发射极电流由下式表达,
$$
I_E=-I_{EF}-\alpha_RI_{CR}
$$
通常来说,$\alpha_R$的值的大致范围为$[0.5, 0.8]$,这个值为管子反过来接时工作的发射极到集电极电流比例。我们可以写出这个时候的电流放大倍数$\beta_R$,如下所示,
$$
\beta_R=\frac{\alpha_R}{1-\alpha_R}
$$
这个值通常在1-5之间,可以看到相比之前的100的电流放大系数,把管子反过用,即原先的E当作C,原先的C当作E,会造成双极型晶体管的电流增益大大降低,其原因在于,双极型晶体管在设计的时候,EC就是不对称的,其目的是为了增大电流放大系数$\beta_F$。把管子反过来接,这个状态被称为Inverse Active Region。
这两个表达式被称为Ebers-Moll等式,之前我就在论文上看到过这个表达式,当时,对这个表达式完全不懂,现在终于明白了其中的来龙去脉。这个表达式可以描述在三个区域中的双极型晶体管的工作情况:
- Saturation Region
- Forward-Active Region
- Inverse-Active Region
$$
I_C=\alpha_FI_{EF}+I_{CR}
$$
$$
I_E=-I_{EF}-\alpha_RI_{CR}
$$
使用下面的表达式,
$$
\alpha_FI_{ES}=\alpha_RI_{CS}=I_S
$$
可以得到一个Ebers-Moll等式的通式,如下所示,
$$
I_C=I_S(exp\frac{V_{BE}}{V_T}-1)-\frac{I_S}{\alpha_R}(exp\frac{V_{BC}}{V_T}-1)
$$
$$
I_E=-\frac{I_S}{\alpha_F}(exp\frac{V_{BE}}{V_T}-1)-I_S(exp\frac{V_{BC}}{V_T}-1)
$$
上面这个表达式通常用于计算机计算管子的大信号行为中。
$I_{CO}$集电极-基极漏电流
集电极基极漏电流由下式表达,
$$
I_{CO}=I_{CS}(1-\alpha_R\alpha_F)
$$
其定义为,当发射极开路时,从集电极漏到基极的电流,通常来说,当BC结处于反偏状态时,这个漏电流的典型值为,25C下,$1pA-100pA$,这个漏电流的大小会随着温度上升而增大,趋势大约为每上升8C,电流增大一倍。所以,这个电流在高温情况下,可能会相当大,大到不可以被忽视的程度。
基极电流表示成集电极电流和集电极漏电流的形式的表达式如下所示,
$$
I_B=\frac{I_C}{\beta_F}-\frac{I_{CO}}{\alpha_F}
$$
注意到两者是反号的,所以温度上升,集电极漏电流增大,会直接导致基极电流变小。
晶体管击穿电压
这部分内容目前应该没有需求,以后再看。
晶体管电流增益$\beta_F$随工作区域的变化情况
大多数一阶分析都做了$\beta_F$是一个常量的假设,但实际上,$\beta_F$是温度和工作区域的函数,如下给出了$\beta_F$的曲线。
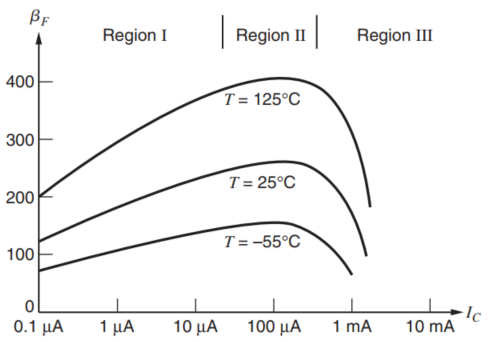
很显然,随着温度的上升,电流增益$\beta_F$逐渐增大,典型的$\beta_F$的温度系数为7000ppm/C。基本原理是,随着温度上升,相同掺杂浓度的射极的电子和空穴发生重新结合的概率更低,增强了发射极电子到达基极的概率,即,提高了发射极注入效率$\gamma$,更多的电流从发射极到达了基极,最终提升了$\beta_F$。
上图还给出了$\beta_F$与集电极电流$I_C$之间的关系,在I区域中,电流很小,$\beta_F$与电流成正比;在II区域中,电流中等,在这个区域中,$\beta$基本保持恒定;在III区域中,电流很大,在这个区域中,电流增大,电流增益$\beta_F$降低。
接下去是一个很有意思的图标,作者通过电流的对数图,说明了$\beta_F$与集电极电流的关系的原因,如下图所示,因为我们感兴趣的量是两个变量的比值,所以通过对数图,可以直接在图上看到比值的变化情况,就是两个曲线之间的距离,这是今后在分析电路图表的时候可以使用的一个方法。
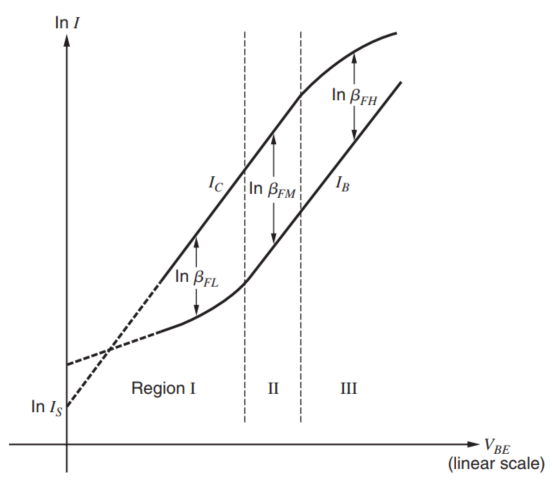
对于基极电流来说,有两个部分,一个是由于BE结上的浓度差导致的空穴移动造成的电流,还有一部分是由于基极在向集电极运输载流子的过程中,空穴和电子发生重新结合造成的电流分量。第一部分的电流由下式表达,
$$
I_B=\frac{I_S}{\beta_{FM}}exp\frac{V_{BE}}{V_T}
$$
第二部分的电流由下面的式子表达,
$$
I_{BX}=I_{SX}exp\frac{V_{BE}}{2V_T}
$$
当集电极电流比较低时,基极电流主要由第二部分主导;当集电极电流比较高时,基极电流主要由第一部分主导。
另一方面,当电流比较大的时候,集电极电流在集电极产生拥塞现象,由于high-level injection以及kirk effect造成集电极电流下降的现象。
总结一下
- 晶体管的电流放大倍数$\beta_F$在管子Forward Active状态下是最大的,在管子Inverse Active状态下会大幅下降
- 晶体管的电流放大倍数$\beta_F$与温度成正比,温度系数大约为7000ppm/C
- 晶体管的电流放大倍数$\beta_F$在中等电流时最大,当电流很小或者是电流很大时,都会下降,因此,要控制好三极管的电流大小,保证足够的电流放大倍数。
双极型晶体管的小信号模型
模拟电路设计中,信号的量通常与偏置相比非常小,比如反馈电路,在这种电路中,可以采用小信号模型来更加方便地对电路进行手算,当然有更加复杂的模型可以用于计算电路,但是作为模拟设计来说,一个重要的技能就是知道在特定的电路中,模型当中的哪些东西可以在手算过程中予以忽略。
考虑下图中的电路,
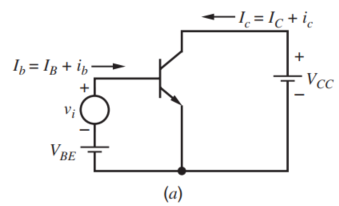
图中,管子处于Forward Active Region,并且将输入施加在基极上,产生了对应的基极电流$I_b=I_B+i_b$,以及对应的集电极电流$I_c=I_C+i_c$,其对应的载流子浓度分布如下图所示,
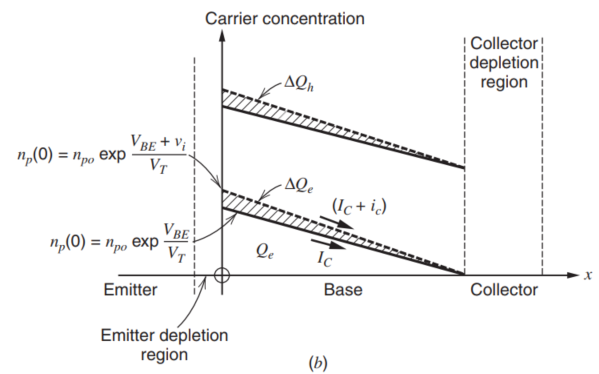
当只有偏置DC电压的时候,载流子浓度的分布如图中实线所示,当基极电压发生小信号波动时,其BE界面上的少子浓度发生变化,导致集电极电流发生变化,接下去推导小信号模型中的参数。
跨导
跨导可以由下面的表达式进行推导,
$$
g_m=\frac{d}{dV_{BE}}I_Sexp\frac{V_{BE}}{V_T}=\frac{I_S}{V_T}exp\frac{V_{BE}}{V_T}=\frac{I_C}{V_T}
$$
可以看到,跨导只与偏置集电极电流有关,并且在25C下,$1mA$的集电极电流条件下,为$38mS$,对应的阻抗为$26\Omega$。有意思的是,这个值对于任意管子,不论是NPN管还是PNP管,不论是什么尺寸,还是什么材料的管子(Si, Ge, GaAs),其跨导都为$38mS/1mA@25C$。
小信号模型的局限性
将大信号模型的表达式如下所示,
$$
I_c=I_Cexp\frac{v_i}{V_T}
$$
进行泰勒展开后有,
$$
I_c=I_C[1+\frac{v_i}{V_T}+\frac{1}{2}(\frac{v_i}{V_T})^2+\frac{1}{6}(\frac{v_i}{V_T})^3+\cdots]
$$
如果输入信号远小于阈值电压,即,$v_i<<V_T$,那么,小信号模型就可以直接使用。总结一下就是,当$v_i=\Delta V_{BE}<<26mV@25C$时,小信号就可以用了。从数量上来看,如果$v_i<10mV$,那么对应的小信号分析的误差就可以控制在10%以内,这是一个比较直观的认知。
基区充电电容
之前的$V_{BE}$变化的MOS管的少子浓度分布图表明,输入信号,也就是$V_{BE}$的变化会导致基区的少子电荷量的变化,$\Delta Q=q_e$。根据电荷守恒原理,基区的多子的数量也会同样增加或减少这么多$\Delta Q_h=q_h$。又因为多子是由基区的信号源提供的,施加$v_i$的信号在基区上就需要提供对应的$q_h$的电荷,这属于电容的特性,因此,基区呈现出如下的电容,
$$
C_b=\frac{q_h}{v_i}
$$
经过一系列推导之后(这一部分推导感觉没有太多学习的意义,因此,不在这里说了),得到了如下的电容值,
$$
C_b=\tau_F\frac{qI_C}{kT}
$$
这里可以得到结论,小信号电容与双极型晶体管的DC集电极电流$I_C$成正比。式子中的$\tau_F$的意义是载流子穿过基极的平均时间,在集成电路中通常是$10ps-500ps$。如果你把管子反过来用,也就是把原先的发射极当作集电极,那么,对应的$\tau_R$会显著变大,对应的基极电容也就变大了,管子就变慢了,这是由于管子两侧掺杂是不对称导致的。处于饱和区的管子的基极电容可以通过$Ebers-Moll$模型来预测,即,将Forward-Active和Inverse-Active的情形做叠加。所以在$SPICE$之类的软件中,常常会有$\tau_R$的参数出现。
输入电阻
双极型晶体管的输入在基极上时,由于基极会有电流流入,所以,会存在一个小信号电阻$r_\pi$,其值由下式给定,
$$
r_\pi=\frac{v_i}{i_b}
$$
又因为$i_c=\beta i_b$,所以得到下面的表达式,
$$
r_\pi=\frac{v_i}{i_c}\beta
$$
接着,又因为$v_ig_m=i_c$,所以有下面的式子成立,
$$
r_\pi=\frac{\beta}{g_m}
$$
这里给出结论,双极型晶体管的小信号输入Shunt Resistance的大小与电流增益成正比,与集电极电流成反比。这里之所以说是Shunt,是因为Shunt在英文中代表了一种低阻支路的含义,这里的双极型晶体管的输入电阻给信号另一条低阻支路,使得管子被Bypass了。
输出电阻
在先前的内容中,描述了在大信号中,$V_{CE}$的变化是如何影响双极型晶体管的大信号特性的,之前说过,当$V_{CE}$产生变化时,会对管子的集电极电流产生影响,由下式表达,
$$
\Delta I_C=\frac{\partial I_C}{\partial V_{CE}}\Delta V_{CE}
$$
根据之前的Early电压的内容,可以知道下面的表达式,
$$
\frac{\Delta V_{CE}}{\Delta I_C}=\frac{V_A}{I_C}=r_o
$$
在这个式子中,$V_A$是Early电压,通常来说这个值在$50V-100V$之间,假设管子的集电极电流为$1mA$,那么对应的输出电阻就在$50k\Omega-100k\Omega$之间。注意到管子的小信号输出阻抗是和集电极电流成反比的,$g_m$是和集电极电流成正比的,因此,$r_o$和$g_m$之间可以互相转换,存在一定的关系,这个关系读者稍微推导一下就可以得到,如下,
$$
r_o=\frac{1}{\eta g_m}
$$
其中,$\eta$的值如下,
$$
\eta=\frac{V_T}{V_A}
$$
如果我们的$V_A=100V$,那么对应的$\eta=2.6\times 10^{-4}$,其实$1/\eta$就是我们的双极型晶体管的本征增益,大概对应了70dB左右,这里可以看到这个增益只与$V_A$有关,因为$V_T$提供了大约$30dB$的增益,这一部分是固定的,剩下的$40dB$全部由$V_A$提供。
集电极-基极电阻
考虑到之前描述的集电极电压调制基区宽度的情形,当集电极电压上升时,BC结的耗尽区宽度变大,造成基区宽度被压缩,如下图所示。
这时,由于基区电子与空穴重结合效应而产生的基极电流$I_{B1}$由于基区宽度变小而变小,作者说这一部分由于$\Delta V_{CE}$变化造成的$I_B$电流变化的效应,由集电极到基极的电阻来进行建模。这里的合理性我还不是特别清楚。下面给出具体的数学表达,
$$
r_\mu =\frac{\Delta V_{CE}}{\Delta I_{B1}}=\frac{\Delta V_{CE}}{\Delta I_C}\frac{\Delta I_C}{\Delta I_{B1}}=r_o\beta_0
$$
作者这里给出了由于重结合造成的基极电流和因为多子扩散到发射极形成的基极电流的比例,后者占据了主导,前者在总基极电流中的比例小于10%。因此,$\beta_0$的典型值约为$\beta/10$。对于平面型的管子来说,其基区的重结合效应更加显著,这里其本质上就是平面型管子的基区宽度更宽,造成了重结合效应更显著了,更多从基极输入管子的基区多子与从发射极发射入基区的基区少子发生了结合,造成了基区电流的上升与到达集电极的基区少子载流子的降低,降低了管子的电流放大倍数。这里作者给出了具体的倍数关系,在平面结构中,由于基区宽度变宽造成的基区电流的增大,从而导致由于重结合效应产生的基区电流上升而造成的此部分电流占比上升,其倍数大约为$\beta_0=
\beta/5-\beta/2$。
小信号模型中的寄生
目前仅仅是考虑到了一些直接可以看出来的管子的寄生,但是对于集成晶体管来说,还有很多寄生需要考虑,需要根据下面的集成晶体管剖面图来进行分析。

容性寄生
在前面的章节里说过,在晶体管的所有PN结的界面上都存在一个与电压相关的电容,这个电容的成因是耗尽区的存在。在上图中,三个电容是耗尽层电容,分别是:
- BE界面上的耗尽层电容$C_{je}$;
- BC界面上的耗尽层电容$C_\mu$;
- 集电极与衬底的耗尽层电容$C_{cs}$
BE界面上的耗尽层电容由于发射极的重掺杂,BE结是一个突变结(abrupt junction),其电容可以由下面的表达式很好地进行数学上地表达,
$C_{\mu}=\frac{C_{j0}}{\sqrt{1-\frac{V_D}{\psi_0}}}$
其中,$C_{j0}$是在结的偏置电压$V_D=0$时的结电容大小,$\psi_0$为内建电势,大约为$0.7mV$左右。
BC界面上的耗尽层电容由于掺杂浓度不高,所以是个缓变结(graded junction),当偏置电压很小时,耗尽层的边缘在结面的附近,在这个区域内,掺杂浓度是耗尽层位置的函数,其结特性显示为一个缓变结,因此,其电容跟随位置的变化
$C_{\mu}=\frac{C_{j0}}{^3\sqrt{1-\frac{V_D}{\psi_0}}}$
当偏置电压很大时,集电极的耗尽区一路延伸到集电极的内部,其掺杂浓度是均匀的,这时,分母的根号为平方根。实际应用中,这个电容的根号取值为平方根到5次方根之间,如下所示,
$$
C_\mu=\frac{C_{\mu 0}}{(1-\frac{V}{\psi_0})^n},n\in[0.2,0.5]
$$
第三个寄生电容是集电极到衬底的结电容,这个等到以后需要的时候再重新阅读考虑。
这里作者给出了这三个电容的典型值,$C_{je0}\approx10fF$,$C_{\mu 0}\approx10fF$,$C_{cs0}\approx20fF$,从中可以看出,集电极到衬底的电容要显著得更大。
阻性寄生
这一部分里面最重要的就是基区电阻$r_b$,当集电极电流显著增大时,这个电阻会显著降低,恶化管子的性能。这个现象作者给出了解释,但是我没有看懂,等到以后有机会了再进行深入研究。
完整的双极型晶体管的小信号模型
有了上面的分析,我们可以给出如下的完整的双极型晶体管的小信号模型,
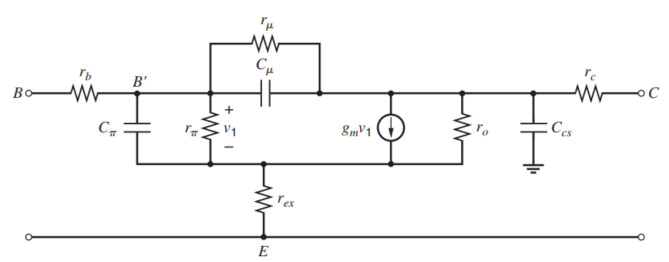
图中的$C_\pi=C_b+C_{je}$,由基区充电电容(基区少子的存在对应存储的多子空穴)以及耗尽层结电容组成。
晶体管频率响应的一些指标
双极型晶体管的高频增益受到小信号模型中的容性器件的大小控制;双极型晶体管的频率能力主要靠衡量管子的短路集电极电流增益掉到1的频率。这个频率称为截止频率(Transition Frequency),这个频率的本质是管子可以被用作放大器的最大的频率。
这个频率可以通过手算来进行分析,使用如下的电路模型,
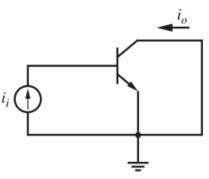
在基极施加一个AC电流,将管子的CE短路起来,测量流入C的电流。如下是该电路的小信号模型,
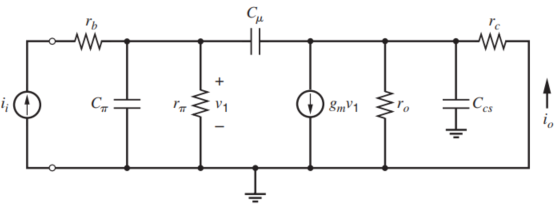
这里为了计算简单,假设$r_c\rarr0$,那么右边的$r_o$和$C_{cs}$就可以认为是被短路了,对电路的传输函数不起到影响,这时,$C_\mu$的右侧为地,$v_1$的电位为$i_1$流过两个电容和一个电阻的并联,如下所示,
$$
v_1=\frac{1}{s(C_\pi+C_\mu)}||r_\pi i_i=\frac{r_\pi}{s(C_\pi+C_\mu)r_\pi+1}i_i
$$
如果通过$C_\mu$的前馈电流可以忽略不计,那么,可以直接写出集电极短路电流$i_o$,如下所示
$$
i_o=\frac{g_mr_\pi}{s(C_\pi+C_\mu)r_\pi+1}i_i
$$
当频率非常大时,上式中的分母中的1可以忽略不计,这时,当电流增益为1时对应的截至角频率$\omega_T$值也可以直接写出,
$$
\omega_T=\frac{g_m}{C_\pi+C_\mu}
$$
转换成频率为,
$$
f_T=\frac{\omega_T}{2\pi}=\frac{g_m}{2\pi(C_\pi+C_\mu)}
$$
双极型晶体管的幅频响应可以由下面的图进行表达,
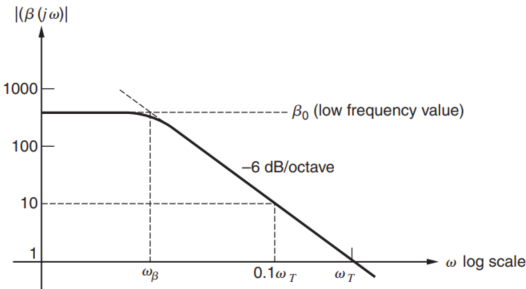
图中的$3dB$折点的频率如下所示,
$$
\omega_\beta=\frac{g_m}{(C_\pi+C\mu)g_mr_\pi}=\frac{1}{r_\pi(C_\pi+C_\mu)}
$$
再来分析一下截止频率的时间常数,如下,
$$
\tau_T=\frac{C_\pi}{g_m}+\frac{C_\mu}{g_m}=\frac{C_b}{g_m}+\frac{C_{je}}{g_m}+\frac{C_\mu}{g_m}=\tau_F+\frac{C_{je}}{g_m}+\frac{C_\mu}{g_m}
$$
因为$g_m=I_C/V_T$,所以,这个时间常数是和集电极电流直接相关的,如果集电极电流很大,那么$\tau_T\rarr\tau_F$。对于低电流的情形来说,$\tau_T\rarr\frac{C_{je}}{g_m}+\frac{C_\mu}{g_m}$,并且会导致截止频率的时间常数上升,也就是说会导致截止频率降低,如下图所示,
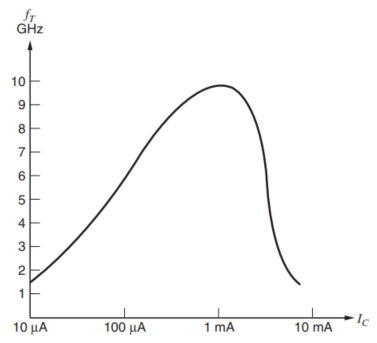
在大电流的情形下,随着电流增大,截止频率也在降低,这一部分无法用我们的简单模型来进行解释。其实,当电流增大时,$\tau_T\rarr\tau_F$,但是当集电极电流进一步增大,$\tau_F$自身会因为之前说到过的高水平注入(High-level injection)和Kirk效应(Kirk Effect)而显著上升,进一步导致截止频率下降;这两个效应之前说过,也会导致电流放大倍数$\beta$显著下降。
MOSFET的大信号模型
MOSFET电路相对于Bipolar电路来说成本更低,与数字电路兼容性更好,于是,在此考虑MOSFET的各种模型。
MOS器件的传输特性
下面是一个典型的增强型N沟道MOS管的剖面图,
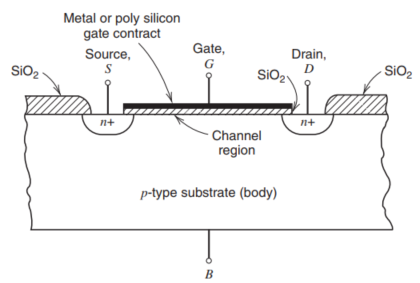
可以看到源和漏是重掺杂的N型半导体,并且在衬底上有一层薄的氧化层,这个氧化层的结构可能是金属或者是多晶硅。
这里我产生了为什么需要使用多晶硅的原因,有几个具体的原因需要考虑:
首先是在设计MOS管的时候,$C_{gd}$电容一直是一个问题,因为在制造过程中,$C_{gd}$或多或少会发生重叠,这时候引入了一个全新的技术,叫做自对齐栅技术(Self Aligned Gate),这种技术先生产栅氧化层,再通过离子注入的技术进行源和漏的掺杂操作,这个过程中,栅氧化层充当了一个隔离膜,防止栅下方的区域被掺杂,从而减小GD之间的交叠。但是这个过程中,需要进行退火(Annealing)操作,这个操作的目的是让晶体重新形成,从而得到想要性质的结构,在掺杂之后,由于加入了一些其他的物质,半导体的电气特性可能被改变,这是加温让其中的粒子重新排布,自己形成对应的晶体结构,提高了结构的性能以及可靠性。由于这个过程中需要高温,大概1000摄氏度左右,这时,如果采用金属例如铝,在660摄氏度左右,这时金属就会融化,从而损坏结构。因此,采用多晶硅可以防止栅的接触发生融化的现象。
另一方面,据网上的说法,采用多晶硅作为接触可以更好地控制MOSfet的阈值电压。
在MOS管的操作过程中,随着栅源电压$V_{gs}$的不断变化,栅下方区域的电导也会发生变化,从而使得可以通过栅电压来控制源漏之间的电流大小。
上图所示的MOS管是增强型NMOS管,增强型说的是在$V_{gs}=0$的情形下,是不存在沟道的,沟道需要被增强从而才能导通,上述的MOS管是由P型半导体作为衬底,形成N型沟道(电子)的增强型NMOS管;我们也可以使用N型半导体作为衬底,形成P型沟道组成增强型PMOS管。当栅源电压为零时,源和漏之间实际上是一组背对背的二极管(Back-to-Back),这种结构造成源漏之间的电阻非常巨大,大概为$10^{12}$的量级。
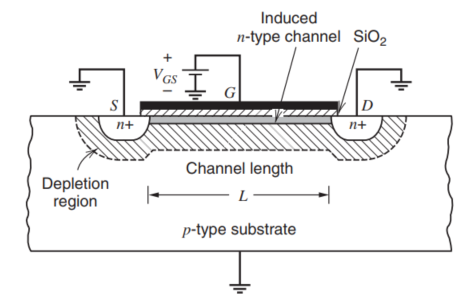
我们考虑如上图所示的情形,这时候,D、S、B全部接地,G接一个正电位栅和衬底之间就形成了由MOS管的氧化层为电解质的一个电容。正电荷存储在栅上,负电荷存储在衬底里(感应出的N型沟道)。
我们使用公式1.10(1.2节中的内容),可以得到耗尽层宽度$X$可以表示为如下的公式,
$$
X=(\frac{2\epsilon\phi}{qN_A})^{1/2}
$$
其中,$\phi$表示了耗尽层中靠近氧化硅界面的电位,$N_A$是P衬底的掺杂浓度,当$G$的电位上升时,对应的掺杂的原子中的空穴被电子填满,造成了空穴被耗尽的情形,这也是耗尽区的本质,基于这一原理,我们可以直接写出耗尽区对应的电荷大小,
$$
Q=qN_AX=\sqrt{2qN_A\epsilon\phi}
$$
当表面电势达到了两倍的费米能级$\phi_f$,反型就发生了,也就是在原本应该是空穴主导的P型半导体的区域出现了电子主导的情形。费米能级由下面的表达式表达,
$$
\phi_f=\frac{kT}{q}ln[\frac{N_A}{n_i}]
$$
上面的表达式可以根据我们之前说的一个班的孩子在一个书架面前比赛谁能够到最高的书的案例进行记忆,其中$kT/q$表示了在某一特定温度下,粒子具有的平均能量,随着掺杂浓度越高,要将一半的粒子加能到导带的能量就越大,这个关系随着掺杂浓度提高会发生对数增长。费米能级电势通常为0.3V,随着在硅中的电势达到0.6V,进一步提升栅中的电压就不会造成耗尽层的宽度发生变化,而会在耗尽层中感应出一层薄薄的电子,这层电子紧贴着氧化层。反型层在源和漏之间形成了一个连续的N型区域,这个区域形成了导电的沟道。这个通道的导电能力会被栅源电压之间的变化所调制。
MOS管的阈值电压由下面的表达式进行表达,
$$
V_t=V_{t0}+\gamma(\sqrt{2\phi_f+V_{SB}}-\sqrt{2\phi_f})
$$
其中,$V_{t0}$为体电压接地时的阈值电压,即没有考虑体效应时的阈值电压,$\gamma$的典型值为$0.5[V^{1/2}]$,从上面的表达式中可以看出,体效应一定程度上会对管子的沟道起到调制作用,但是是根号规律的调制,相比于栅的线性调制来说,要更加弱一些。$V_{t0}$的值实际上是通过在沟道区域中进行掺杂来实现调整的,在沟道中调整P掺杂的浓度可以将管子的$V_{t0}$在0.3V和1.5V之间调整;在沟道中加入N型的掺杂,可以让沟道在$V_{GS}=0$的条件下就处于导通状态。
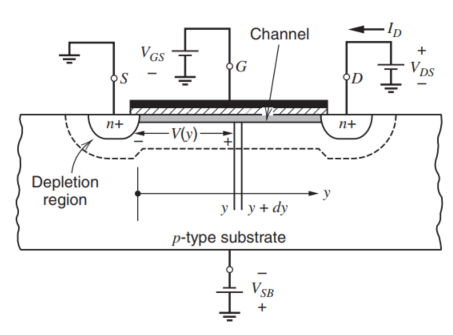
接下来计算n沟道MOSFET的大信号特性,在接下去的分析中,假设S接地,其余端子D、G、B均有对应电位,如下图所示,