写在前面
最近在工作中遇到了一个关于Bandgap的问题,问:如下两个电路,$Q1:Q2=1:8$,其余所有MOS管的尺寸均一致,问哪一个电路是正确的?
我从来没有思考过这个问题,于是,我仔细思考,将思考的过程和结果记录在此博客中,以供之后查看。
方法一
这两个电路中存在一个差分转单端运算放大器,这个运算放大器是由两个NMOS管构成的,NMOS管构成共栅放大器,其中,栅极接收来自下方的Bipolar和电阻组成的网络的输出电压;从其中一个NMOS的漏极产生输出电压,具体的等效电路如下图所示,
可以看到,上面连个电路的区别在于左右两个支路反馈的极性,其中(a)图中的极性分别为右侧支路的反馈为负反馈,左侧支路的反馈为正反馈;(b)图则相反,右侧支路的反馈为正反馈,左侧支路的反馈为负反馈。要搞清楚上面两中反馈的机制到底对电路会产生怎么样的影响,应该先写出电路的电压-电流表达式,先有一个数学层面的感受。
解出下面的电路图中的电压表达式,
由于Bipolar的特性为指数特性,其电流来自于基极的少子的扩散运动,扩散运动来自于BE界面和BC界面浓度的不一致,其中BC界面的浓度可以忽略,基本为零,BE界面的浓度服从Fermi-Dirac分布,可以做Boltzmann近似,得到近似指数的分布,其表达式如下,
$$
I_C=I_Se^\frac{V_{BE}}{V_T}
$$
根据上述分析,在(a)图中,$V_1$的表达式如下所示,
$$
V_1=V_Tln\frac{I_C}{I_S}
$$
在(a)图中,$V_2$的表达式如下所示,
$$
V_2=I_CR+V_Tln\frac{I_C}{nI_S}
$$
我们可以在数学上绘制出这两个点的$V-I$特性曲线,如下所示,
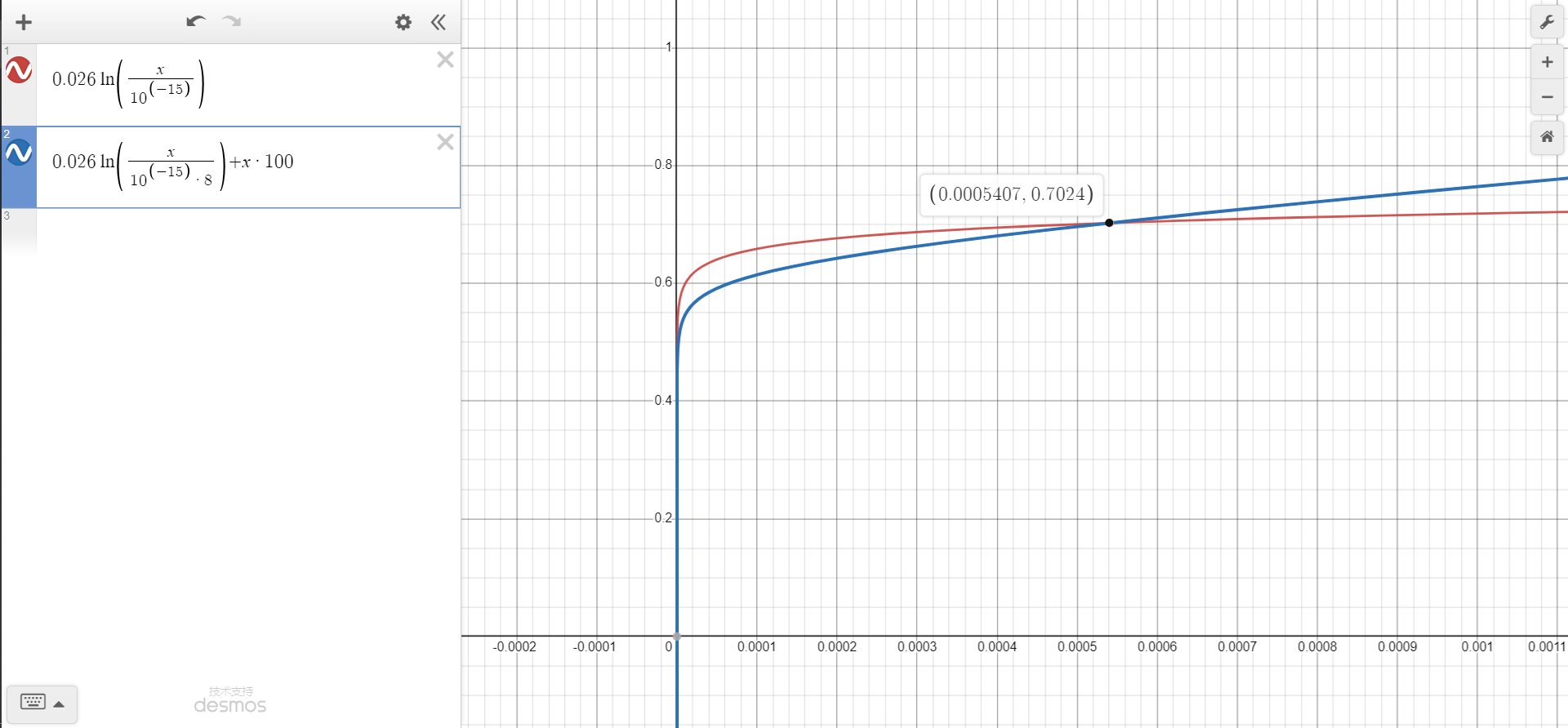
可以看到这两个特性曲线存在两个交点,即存在两个状态,使得电压相等且电流相等。在运算放大器控制下,这两个点都可能存在稳定的工作可能性。这里就解释了为什么Bandgap需要一个启动电路的原因。
接下去我们对$V_2-V_1$关于$I_C$求导,如下所示,
$$
\frac{\partial (V_2-V1)}{\partial I_C}=R+V_T\frac{nI_S}{I_C}-V_T\frac{I_S}{I_C}=R+(n-1)\frac{I_S}{I_C}>0
$$
可以看出,上面的导数的结果,只要保证$n>1$的条件,在我们的案例中$n=8$,就可以保证当$I_C\uparrow$时,一定有$(V_2-V_1)\uparrow$。
所以当我们再看如下这两个电路图时,在(a)图中,当$(V_2-V_1)\uparrow$时,运算放大器的输出增大,迫使$MP1$和$MP2$的栅极电压上升,从而流过$MP1$和$MP2$的电流下降,即,使得$I_C\downarrow$,从而使得$(V_2-V_1)\downarrow$,逆转原先的增大趋势,形成负反馈,最终电路趋于稳定。

再来看在(b)图中,当$(V_2-V_1)\uparrow$时,运算放大器的输出降低,迫使$MP1$和$MP2$的栅极电压下降,从而流过$MP1$和$MP2$的电流上升,即,使得$I_C\uparrow$,从而使得$(V_2-V_1)\uparrow$,形成正反馈,最终$(V_2-V_1)$的值会越来越大,导致电路不能正常工作。
总结一下
这篇文章总结了Bandgap电路的工作特性,主要说明了Bandgap电路中的反馈极性的分析问题,以及电路中的稳定点存在两个的问题,从数学上证明了这两个问题的结果。
最后,让我们从直观的理解上,分析一下为什么随着电流的增大,$V_2-V_1$会越来越大。本质上是因为电阻的$V-I$特性是线性的,而Bipolar的$V-I$特性是对数的,对数的关系要弱于指数的关系,而$V_2$中的对数成分由于比例关系$n$的存在,而形成了一个更加弱的对数关系。从这个角度来看,我们可以认为$V_2$完全由线性关系主导(当然,实际情况并不是如此),而$V_1$则是由一个对数关系主导的。由于对数关系的关联性要弱于线性关系,所以,$V_2$对变量$I_C$对的耦合程度要远大于$V_1$对变量$I_C$的耦合关系。
让我们再从直观的角度来看一下为什么电路存在两个稳定的工作点,我们可以直接绘制出如下的电压电流关系图,
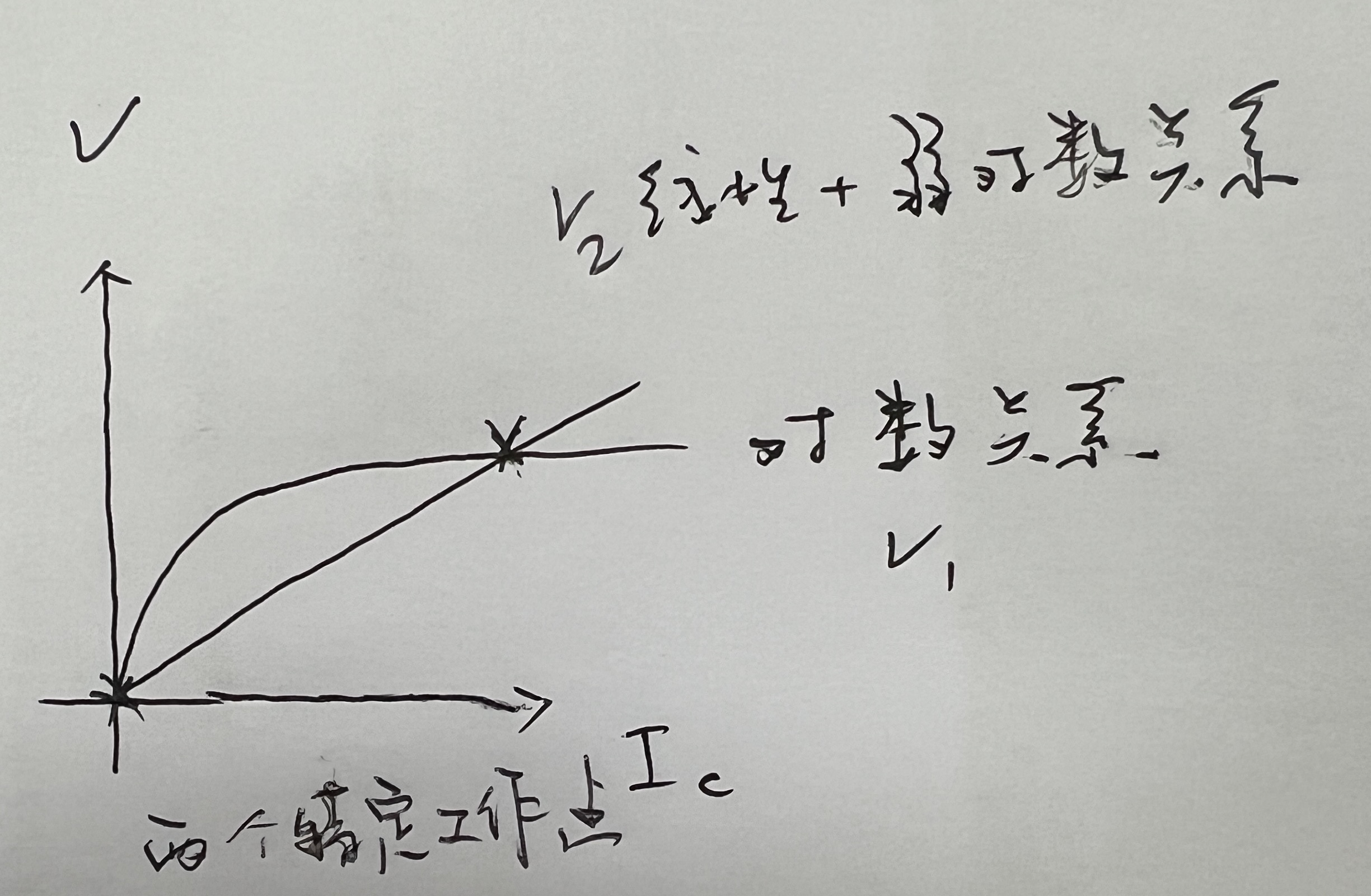
可以很明显的看到,这两个$V-I$特性曲线存在两个交点。
到这里,我们分析了两个我从来没有考虑过的问题,解决了之前仿真过程中一直困扰我的两个问题,在此记录一下,以供未来查阅。
方法二
最近同学又告诉我了一种新的分析方法,在此总结一下,以供之后参考。这种分析方法将整个电路的正反馈环路进行了分析,假设在输入对管的栅极上存在一个电压,如下图所示,

案例一
在(a)的案例中,信号经由MN2的栅极->MN2的漏->MP2的栅->MP1的漏->MN1的栅,这个环路进行运作,在这个环路上,我们先给出由MN2的栅到MN2的漏的表达式,这时候,MN2管的跨导由于源退化电阻的存在,导致跨导减小了,
$$
G_1=\frac{-g_{mN}}{1+g_{mN}(R+1/g_{mQ})}\frac{1}{g_{mP}}
$$
其中,$g_{mQ}$为双极型晶体管的跨导。接下去我们再计算从MP2的栅到MP1的漏的表达式,
$$
G_2=-g_{mP}(1/g_{mN}+1/g_{mQ})
$$
将上述两个增益乘起来,得到如下的总增益,
$$
G=G_1G_2=\frac{g_{mN}(1/g_{mN}+1/g_{mQ})}{1+g_{mN}(R+1/g_{mQ})}
$$
假设$g_{mN}:g_{mQ}=k$,那么,上面的表达式可以化简为如下,
$$
G=\frac{1+k}{1+k+g_{mN}R}
$$
三极管的跨导$g_{mQ}$与MOS管的跨导$g_m$之间的关系
一般来说,三极管的跨导的表达式如下所示,
$$
g_{mQ}=\frac{I_C}{V_T}\approx40I_d
$$
这个跨导在我的”PaulGray经典著作读书笔记第一章”的阅读笔记里面有提到,这个跨导只与电流和温度有关,与双极型晶体管采用的材质、尺寸、型号(PNP or NPN)都是无关的。
对于处在饱和区的MOS管来说,其跨导可以使用下面的表达式表达,
$$
g_m=10I_d
$$
对于亚阈值区的器件来说,$I_d$与$V_{gs}$的关系如下,
$$
I_d=I_0e^{\frac{V_{gs}}{\zeta V_T}}
$$
其中,$\zeta>1$,相当于在亚阈值区的器件基本可以视为三极管,但是其等效热电压会更高,对应出的跨导表达式如下所示,因此,其跨导也就更小,
$$
g_m=\frac{I_d}{\zeta V_T}\approx\frac{40I_d}{\zeta}
$$
因此,一般来说,$g_{mN}:g_{mQ}=k$,其中,$k\in(0,1)$
再回到我们的增益表达式,如下所示,
$$
G=\frac{1+k}{1+k+g_{mN}R}
$$
这个表达式的取值范围为$G\in [0,1]$,说明在这个电路的配置下,正反馈的回路表现为对信号的衰减,其增益小于1。
案例二
我们再来看另外一种情况,如下图的b所示,

在这种情况下,信号由MN1的栅->MP1的漏->MP2的栅->MN2的漏->MN1的栅这一正反馈回路传递,我们先计算一下由MN1的栅到MP1的漏的增益,
$$
G_1=\frac{g_{mN}}{1+g_{mN}(1/g_{mQ})}\frac{1}{g_{mP}}
$$
我们再来计算由MP2的栅到到MN2的漏的表达式,如下所示,
$$
G_2=g_{mP}(1/g_{mN}+R+1/g_{mQ})
$$
当我们把上面的两个表达式写在一起时,可以得到如下的表达式,
$$
G=G_1G_2=\frac{g_{mN}(1/g_{mN}+R+1/g_{mQ})}{1+g_{mN}(1/g_{mQ})}
$$
将关系$g_{mN}:g_{mQ}=k$代入表达式后,可以得到如下的表达式,
$$
G=\frac{1+k+g_{mN}R}{1+k}
$$
从这个表达式中,可以发现,这种电路配置下,正反馈环路的增益大于1,使得电路会产生不稳定的情况。
总结一下
我们可以现在总结一下这两个电路的异同,这两个电路的区别在于,正反馈回路最一开始的跨导很重要,其决定了电路的增益。如果需要抑制正反馈环路的增益,需要在环路最开始的跨导上应用源退化电阻,也就是(a)电阻,从而使得跨导降低,降低正反馈环路的增益大小。从公式上来看,源退化电阻会导致$G_1$的增益中的跨导部分降低一定的倍数;然而另一侧的源退化电阻会导致$G_2$的增益中的负载部分上升一定的倍数。如果要使增益小于一,则要令增益中降低的倍数大于上升的倍数,因此,在产生$G_1$增益的一侧要应用更大的源退化电阻,因为两个三极管的$g_{mQ}$的值一样,所以源退化电阻大的支路是存在电阻的一侧。自然,为了保证一开始的跨导在电阻一侧,所以电阻一侧的PMOS负载应为二极管连接型。

