写在前面
这段时间有太多事情阻碍了我的阅读进程,现在快要过年了,本人终于可以继续进行愉快的经典阅读了。这一部分我觉得是挺重要的,之前我都是进行探索式的学习来了解的,这是第一次通过教材来进行这一部分内容的阅读。前言中最重要的一句话是:Jitter和Power是一对折中
Noise简介
时域和频域中的噪声
噪声是随机过程,任意时刻的噪声大小是不可预测的,一般噪声的幅度符合高斯分布。我们可以利用噪声的幅度的概率密度函数来对噪声进行量化,如果概率密度函数符合高斯分布,我们可以使用$\sigma$来对噪声进行量化描述。由于频域中的频率分辨率取决于样本的时间长度,因此,如果要想频谱中的噪声谱线是一个连续的曲线,那么我们的样本的时间长度就要趋近于无穷大,这是不现实的。这里我们使用噪声功率谱密度的概念来解决这个问题,我们把这一曲线定义为$1Hz$频带内的噪声总功率。
器件噪声
在CMOS工艺中,比较重要的是电阻和MOSFET的噪声,电阻的噪声功率谱密度表示如下,
$$
V_n^2=4kTR\space \space V^2/Hz
$$
其物理模型可以表示为如下,

MOSFET还会产生闪烁噪声,这个噪声的功率谱密度和管子的尺寸成反比,和频率成反比,换句话说,管子越大,闪烁噪声的功率谱密度越小;频率越高,对应的噪声功率谱密度越小,由下面的表达式表达,
$$
S_{1/f}(f)=\frac{K}{WLC_{ox}}\frac{1}{f}\space \space V^2/Hz
$$
MOS管的热噪声由下面的表达式表达,
$$
I_n^2=4kT\gamma g_m\space\space A^2/Hz
$$
噪声的传递
噪声的传递函数如何计算呢?可以把噪声视作一个理想源,然后计算从这个源到输出的噪声传递函数$H(f)$,下面给出的表达式可以写出噪声作用体现在输出的结果,
$$
S_{n,out}(f)=S_{n1}(f)\cdot|H(f)|^2
$$
噪声的平均功率
对于一个周期信号,信号的平均功率表示如下,
$$
P_{x1}=\frac{1}{T}\int^{T/2}_{-T/2}x_1^2(t)dt
$$
从频域角度来看,功率可以表示为噪声功率谱密度曲线的积分,如下所示,
$$
P_{x2}=\int^{\infty}{-\infty}S{x2}(f)df
$$
直观来说,噪声总功率就是功率谱密度曲线下方的面积
噪声在时间上的累积
噪声样本的时间长度决定了噪声频谱的频率下限和对应的频率分辨率,所以给噪声加窗(矩形窗),意味着给噪声施加了一个高通滤波器。这个高通滤波器对应低于$1/(\pi t_a)$的频率有一个近似$\pi t_af$的增益。这个观点在后面分析cycle-to-cycle jitter的内容时,非常有用。
基本的抖动和相位噪声的概念
抖动
抖动是一个时间的概念,描述了信号的过零点偏离理想值的大小,抖动是一个时间上的概念。通常来说,眼图是一个很好的直观上来观察抖动的一个工具。但是,时域上的工具并不能很好地观察抖动时确定性的还是随机的,因此,通常采用频域手段来区别各种不同的抖动。
在LC振荡器中,电源电压会对振荡频率进行调制,这是因为输出的共模电平基本就是VDD,如果VDD波动,那么会调制$C_{DB}$这个电容,从而通过输出看到的电容大小波动来对频率进行调制。具体可以看这一节的案例,在44页。
相位噪声
phase noise和jitter的主要区别在于,phase noise通常指随机的过零点抖动,而jitter里面有确定的抖动,也有随机的抖动,也就是jitter是一个更大的概念。并且,phase noise通常是一个频域的概念,我们会使用频域的工具来定量描述phase noise的大小。下面对相位噪声进行一个定性的观察,
$$
V_{out}(t)=V_0cos[\omega_0t+\phi_n(t)]=V_0[cos\omega_0tcos\phi_n(t)-sin\omega_0tsin\phi_n(t)]
$$
假设$\phi_n(t)$足够小,那么,我们可以得到假设$sin\phi_n(t)=\phi_n(t)$,$cos\phi_n(t)=1$,这就是窄带FM近似,使用上面的这个近似,我们可以得到下面的公式,
$$
V_{out}(t)=V_0cos\omega_0t-V_0sin\omega_0t\phi_n(t)
$$
我们可以发现相位噪声的时域函数和信号的时域函数在时域中相乘,在频域中意味着将相位噪声的频谱搬移到对应的信号频率上,这也解释了为什么有相位噪声的波形会出现频谱上的裙摆。
相位噪声如何计算呢,我们先确定对应的频偏,接着,计算单位频率内的噪声功率,接着,将所有这些频偏上计算出来的噪声功率谱密度归一化到载波频率,最后对这个比例取dB,就可以得到最后单位为$dBc/Hz$的相位噪声功率谱密度图。
下面给出一个热噪声施加在VCO上的案例,如下所示,
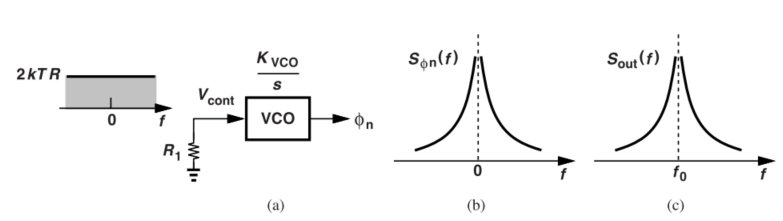
其相位噪声功率谱密度如下计算,
$$
S_{\phi_n}(f)=2kTR_1(\frac{K_{VCO}}{2\pi f})^2
$$
这里有几个注意的地方,一个是这边的相位噪声功率谱密度是双边的,所以,并不是所谓的$4kTR$,这个要特别注意;第二个是热噪声在经过VCO之后,都会变成$1/f^2$的函

