写在前面
本书是Abidi的博士学生缩写,其内容很有参考意义,作为频率综合器的研究人员,非常值得一看,并且反复学习。
前言
本文主要提供了一个不同的视角来设计振荡器,用这种方法来解决怎么看待振荡器的噪声的问题。
本书第一节主要是描述一些基本概念和动机问题;第二节概括了以下相位噪声、时间抖动的基本概念,并且给出了一些早期的分析噪声的方法;第三节和第四节以Colpitts振荡器和电流偏置振荡器为例,分析了相位噪声产生背后的物理机制;第五章讨论了;第五章主要是讲LC振荡器的设计折中问题;第六章和第七章主要是讨论了振荡器中通常被忽略的噪声来源:闪烁噪声。
第一章
振荡器的噪声分析从最初的leeson公式,再到可以预测实际情况的仿真工具的出现,再到Huang的噪声显式表达式的工作的出现,经历了一个过程,本文所作的工作从上述的这些工作中都获得了许多灵感。
振荡器的数学模型
$$
v(t)=A(t)sin(\omega_0t+K_v\int_0^t v_c(u)du)
$$
其中,$v_c(u)$是振荡器控制电压的函数,是时间的函数。振荡器的瞬态频率由下面的表达式给出,
$$
\omega(t)=\omega_0+K_v v_c(t)
$$
可以想象,控制线上的电压的任何扰动都会导致瞬态的频率偏移,这种频率偏移会在时间上进行累计,噪声相位随着时间不断累计,最后发散开来,趋于无穷大。
LC振荡器中的附加白噪声
一个震荡只会收到两个变量的控制,一个是幅度,还有一个是相位。当白噪声叠加到震荡上,会对这两个变量同时造成影响。
(这一部分的推导我截屏如下,本人因为水平原因暂时没法看The Designer’s Guide to High-Purity Oscillators懂,待日后再回来看并总结)

线性振荡器
在这个部分我们将会使用线性系统理论给出一个错误的推导过程,之后会进行解释为什么这一部分是有问题的。
将线性系统应用于振荡器
振荡器本质上是不线性的,它能在稳定的幅度下进行振荡完全是因为其的非线性。线性模型用来分析振荡器的震荡条件是可以的,但是振荡器在某个特定频率下稳定振荡的情形与线性模型完全不同,并且,线性模型也没有办法预测振荡器的幅度。线性模型可以获得一个震荡条件以及估计稳定振荡时所处的频率。
线性振荡器的噪声分析
我们可以使用振荡器的线性反馈模型来进行推导噪声的传递函数,如下所示,
$$
|H(\delta\omega)|^2=(\frac{\omega_0}{2Q\delta\omega})^2
$$
如果白噪声作为激励源,可以在输出得到如下的噪声的功率谱密度,
$$
L_{out}(\delta\omega)=4kTFR(\frac{\omega_0}{2Q\delta\omega})^2=\frac{ktFR}{P_0}(\frac{\omega_0}{Q})^2\frac{1}{\delta\omega^2}
$$
上述表达式就是著名的leeson公式,上述推导过程就是存在问题的,使用了线性模型进行推到的,并且它还是时不变的。这就意味着如果噪声的频率低的话就很难实现噪声到相位噪声的转换,也就是这个模型无法建模闪烁噪声,只能建模振荡频率附近的噪声。这种模型给出的噪声对幅度和相位的贡献是一样的,但是后面很快可以看到,有些部分的噪声只会对相位有贡献。
接下去我们会详细推导上面的线性模型错误的原因。
第二章
在正弦波里面,通常振荡的质量只取决于频率,而不取决于幅度,这是因为在电路里面通常过零点是我们关注的信息,也就是时间戳,这个只与正弦波的频率有关。
信号抖动的测量可以分为两类:确定性抖动和随机性抖动。确定性抖动来自于那些有很多杂散的信号,这些信号的频率位置是固定的,有固定的频率偏移。随机的抖动来自信号相位的随机变化,体现为信号的裙带。实际里面,对于RF接收器来说,幅度上的波动对于应用来说,并没有什么影响,因为混频器对幅度波动不敏感;但是对于RF发射器来说,幅度上的波动会进入相邻的信道,产生干扰。因此,对于RF接收器来说,幅度波动是我们不关注的,但是对于发射机来说,幅度上的波动可能是我们需要关注的。
时域抖动
如果给定一个阈值,信号会每$T$秒穿过这个阈值一次,则称这个振荡的周期为$T$,在实际中,信号过零点的位置总是在左右抖动,从统计学角度讲,振荡的波形是一个由下面公式表达的随机过程,
$$
V(\phi_n,t)=Asin(\omega_0t+\phi_n)
$$
表达式中的$\phi_n$是一个产生随机相位波动的随机过程。
如果我们现在评估第N个时间戳的时刻的偏移的统计量,那么,我们应该把每一个时间戳的随机量相加得到一个新的统计量。如果我们假设随机波动产生的抖动是白噪声,服从正态分布,那么随着时间的增长,时间戳的方差会越来越大,且线性增长,因为随机噪声是Power(Variance)相加,这也是为什么一个free running的OSC最终的绝对抖动会趋于无穷大的原因。我们把某时刻的相对于理想的时间戳的时间差称为绝对抖动。它衡量了相对于一个理想无噪声源来说,时域抖动的累积。McNeil给出了绝对抖动方差的表达式:
$$
\sigma_\Delta^2=\kappa^2t
$$
$\kappa$是时域中振荡器的品质因素,Q值越大,$\kappa$越小,绝对抖动的方差就越小。对应的绝对时域抖动的相位抖动由下面的表达式表达,
$$
\theta_n=2\pi \frac{\Delta_n}{T}
$$
注意这个量仅仅在过零点评估,不像之后讨论的相位噪声,这个相位噪声是定义在所有时间上的。
上文所述的绝对抖动的方差表达式还可以写做下面的表达式,
$$
\sigma_\theta^2=2Dt
$$
D被称为扩散系数,这里借用了扩散的概念,在频域上表现为频谱发生了扩散,这个概念后面还会用到。
我们之前强调过,一个没有约束的振荡器的绝对抖动不收敛,将会趋于无穷大。注意,这里我们做了一个假设,就是每一个周期的统计量都是互不相关的,这样他们的方差才能够直接相加,这就意味着闪烁噪声没有考虑在内。闪烁噪声是有记忆效应的,一个周期的抖动会取决于先前的抖动的统计量的结果。如果有一个锁相环对振荡器进行控制,那么绝对抖动就不会趋于无穷大,它一开始会随着时间增大,最后达到锁定后,绝对抖动的方差就不再增长了,如下所示,
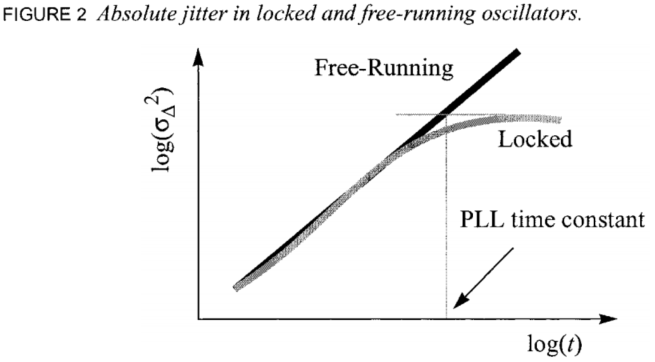
绝对抖动讲完了,接下去就是一个更有用的概念,cycle-to-cycle jitter,或者周期抖动,其表达式如下,
$$
\sigma_j^2=\kappa^2T
$$
和之前我们说的抖动方差的概念是差不多的,衡量了一个周期的抖动的统计量。
认识相位噪声
可以使用如下图所示的Phasor结构来分解噪声,可以把噪声分解为平行载波的部分和垂直于载波的部分,平行于载波的部分只会改变信号的幅度,通常是我们不关心的;但是垂直于载波的部分会改变相位,是我们感兴趣的部分。

作者对这一部分的数学推导有一些让我迷惑的地方,无法理解。
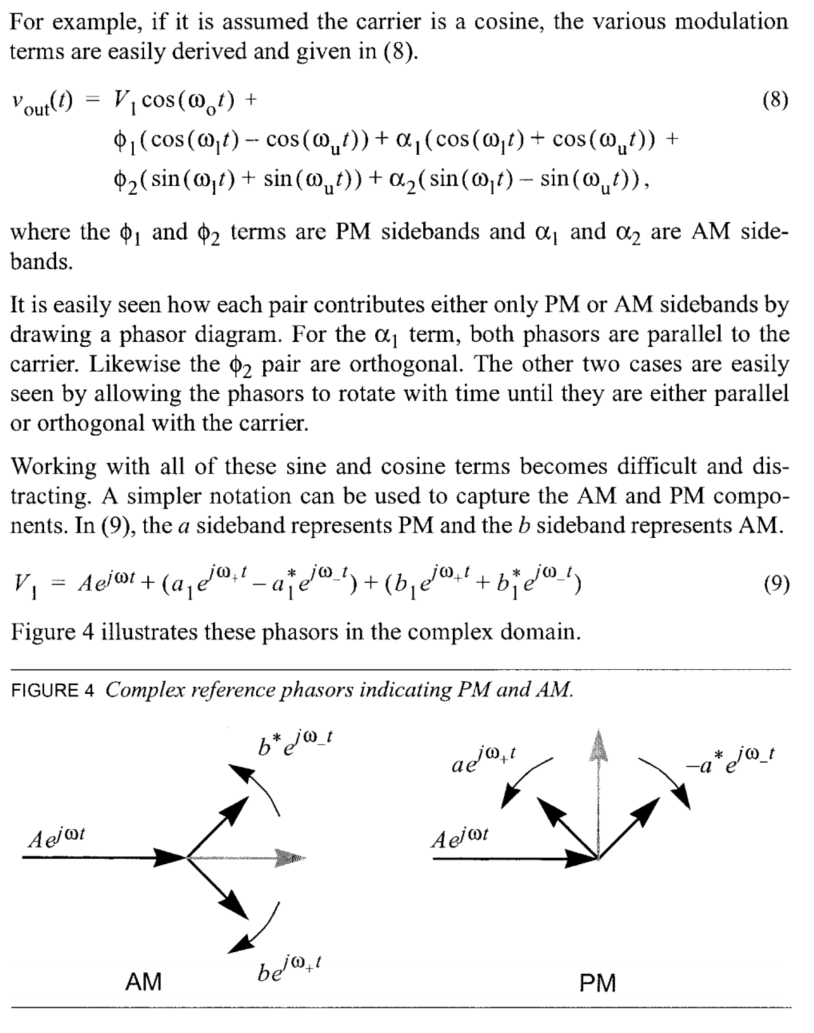
等到看完书之后再回来看一下。
电流偏置振荡器
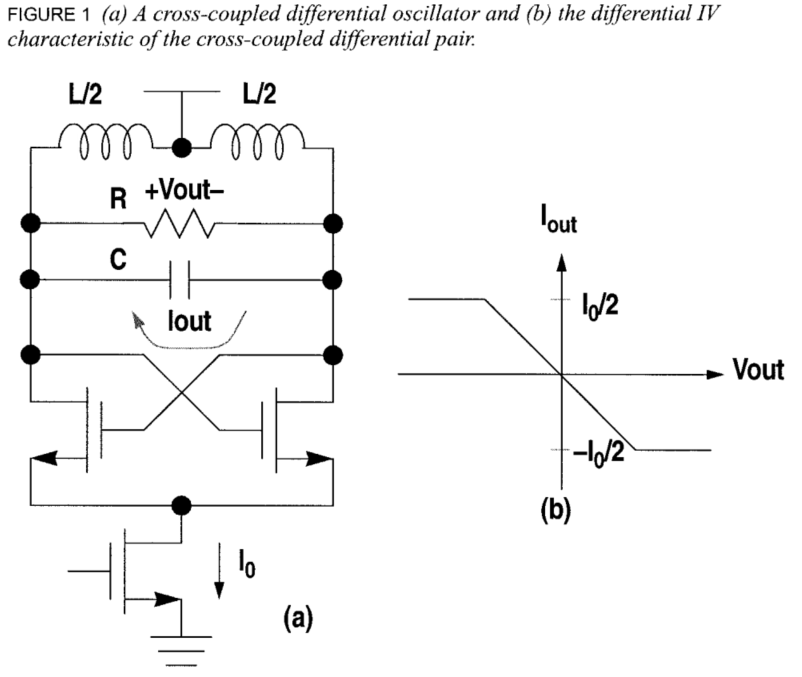
上图是一个典型的LC振荡器的原理图,这个电路是全差分的电路,整个电路由下方的电流源提供偏置。这里面的电感是差分电感,其本质原因是因为差分电感面积更小,并且可以有更高的Q值。交叉耦合对的IV特性由上图中的右侧曲线表达,在斜线部分,电路对外提供负阻,在平线区域,电路对外的不提供任何负载。
当振荡器处于稳态,也就是其处于稳定振荡的状态时,振荡控制差分对的MOS管的开启与关闭,产生一个差分的方波电流,这个方波电流有一个基波分量,其大小为方波摆幅的$4/\pi$倍。谐振器滤除了高阶的信号分量,只有基波流过电阻。如下图所示,最终产生了一个幅度更大的正弦波。
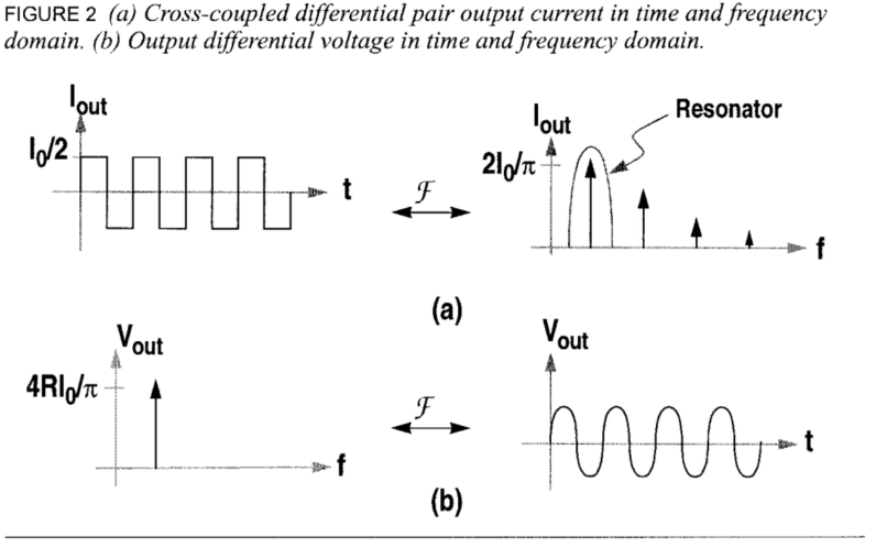
最终输出电压的幅度如下所示,
$$
V_{out}=\frac{2}{\pi}RI_0
$$
当增加尾电流源的电流时,电路输出的幅度会如下图所示不断增长,最终到达最大值。在这时,电流源的管子会被压入线性区,这个过程可以简单描述为电流源提供了巨大的电流,超过了振荡器可以承受的电流后,被压入线性区,变成了一个小电阻,近似接地。
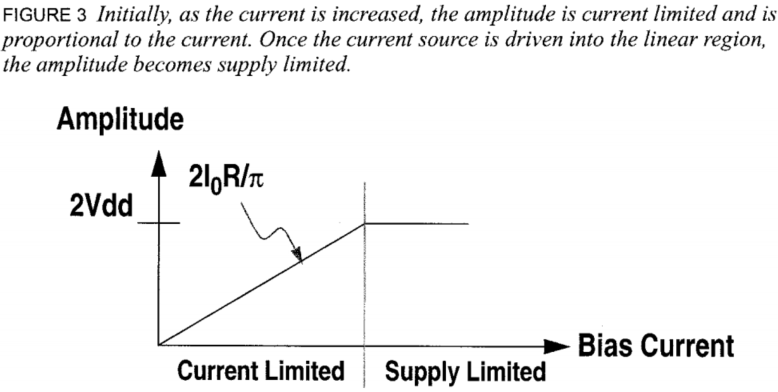
差分振荡器的线性分析
LC振荡器的相位噪声通常通过leeson公式中的比例来进行定义,该公式如下图所示,
$$
\mathcal{L}(\omega_m)=\frac{4FkT}{V_1^2}(\frac{\omega_o}{2Q\omega_m})^2
$$
通常上面的表示会改写成下面的形式,
$$
\mathcal{L}(\omega_m)=F\frac{1}{V_1^2}\frac{kT}{C}\frac{\omega_o}{Q}\frac{1}{\omega_m^2}
$$
上面表达式里面的F通常是一个与电路有关的放缩系数。考虑下面的图,理想的负阻等于LCtank里面的实际电阻,所以贡献了相等的噪声,但因为负阻并不是一个线性电路,其噪声的缩放系数设置为$\gamma$,因此,整个电路的噪声缩放系数为$1+\gamma$,如下图所示。
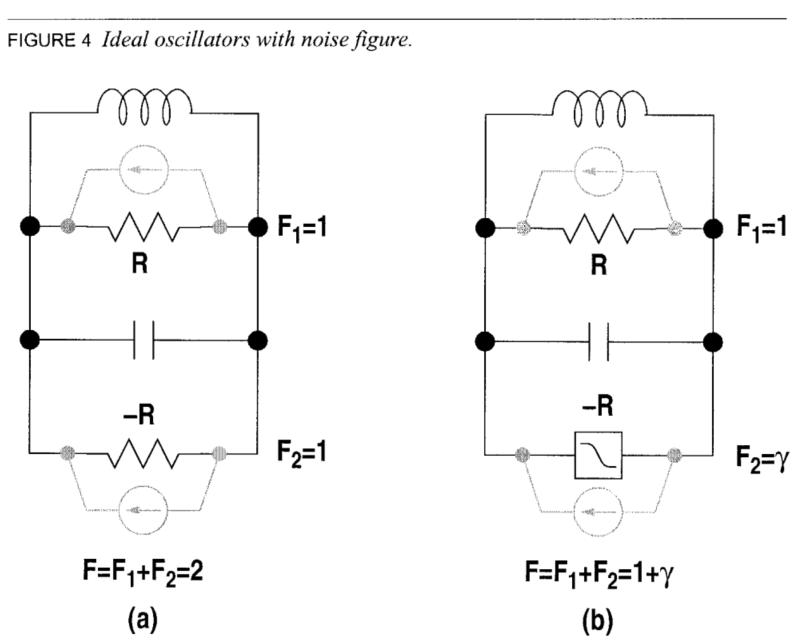
由热噪声引入的相位噪声
在频偏较大的位置,相位噪声的主要来源是因为热噪声。曾经有许多方法来分析这个过程,但是没有一个方法足够简单,没有一个方法可以进行手算。这里提出一个方法。这个方法利用了一个非线性电路的性质来简化分析。如果一个窄带相位调制的信号施加在一个没有记忆的非线性电路上,并且它之后接入了以恶搞中心频率为载波的窄带滤波器,那么其输入如果存在一个边带,输出这个边带会以相同的功率比存在。
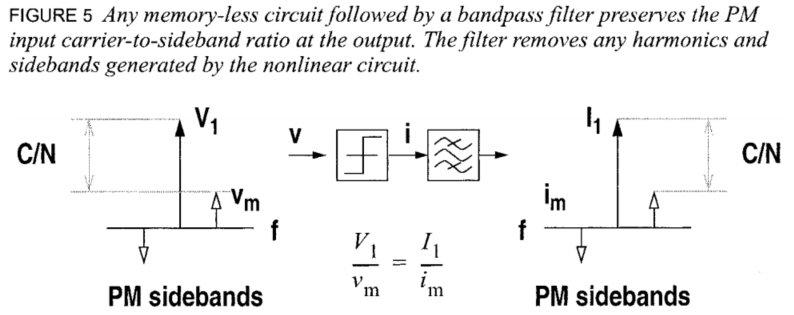
上面这个性质的意义在于说明,在非线性电路中,如果没有任何感抗器件,那么就不会存在AM向PM的转换。
下面作者使用一系列推导来说明了在VCO电路里面,不会发生AM到PM的分量的转换。这部分推导我先忽略了,作者换句话说,也就是如果差分对的输入上叠加了一个振荡源,这个源上有多少相位噪声,那么输出就会产生多少相位噪声,这一性质可以帮助简化分析。
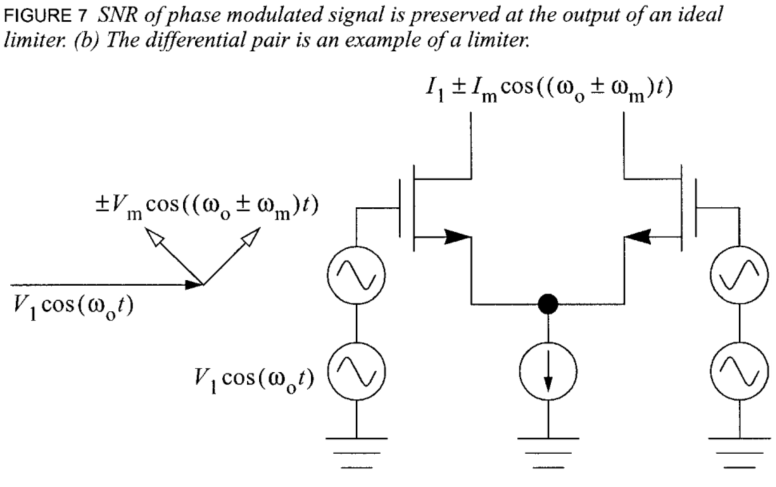
谐振器噪声
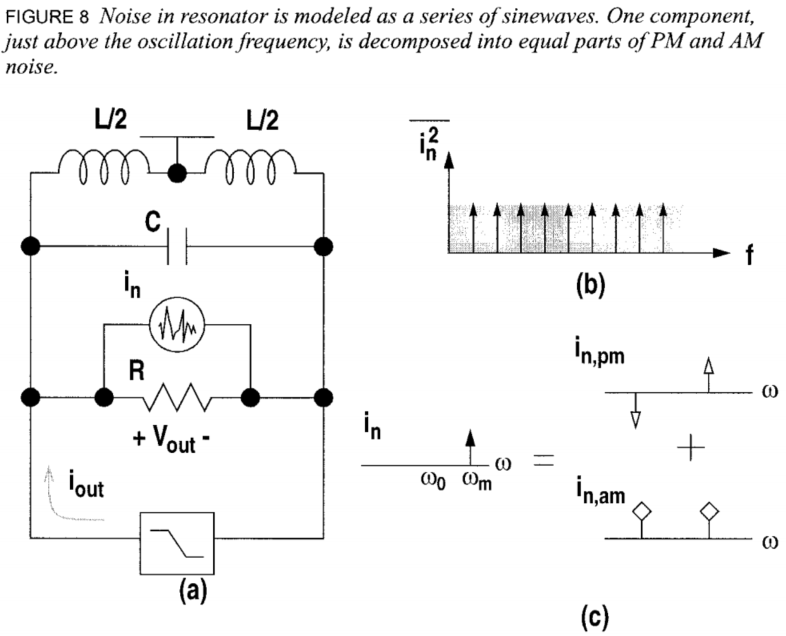
如上图所示,噪声可以分解为一系列不同频率得正弦波,我们先考虑在载波频率附近的一个正弦波,这个正弦波可以被分解为PM边带和AM边带。
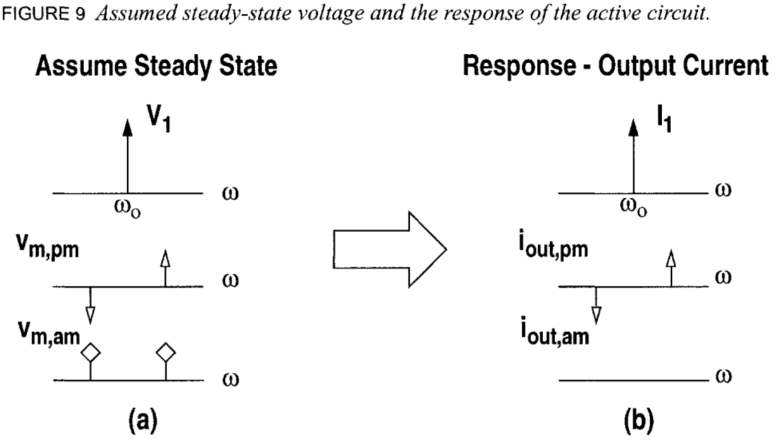
首先我们先假设在稳态下,谐振器上已经产生了振荡。它周围有如上图所示的一些未知的PM和AM边带。经过差分对后产生对应的电流相应,根据先前的分析,AM部分没有了,只剩下了PM的部分。

