写在前面
为什么要了解DSM(Delta-Sigma Modulator)呢?因为在我们的ADPLL里,存在DCO的量化噪声,这个量化噪声按照最低可实现的最小频率LSB计算,也不能满足我们的应用需求,(见”ADPLL相位域MATLAB模型”这篇文章)这时候,我们考虑采用DSM将带内量化误差水平降低,达到降低抖动的目的。
了解DSM的前世今生
此部分内容源自于下面的文献
B. Razavi, “The Delta-Sigma Modulator [A Circuit for All Seasons],” in IEEE Solid-State Circuits Magazine, vol. 8, no. 2, pp. 10-15, Spring 2016, doi: 10.1109/MSSC.2016.2543061.
DSM的前一代产物是DM,全程为Delta Modulator,如下图所示,
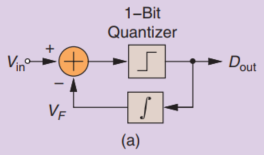
假设我们的量化器只提供量化噪声,那么整体环路的传输函数主要由积分器决定,假设积分器有增益$A$,那么积分器的线性模型如下所示,
$$
H_{sum}=\frac{A}{s}
$$
那么环路的输入-输出的传输函数为,
$$
H_{CL}=\frac{1}{1+H_{sum}}=\frac{s}{s+A}
$$
从上述传输函数中可以看到,在$\omega<A$的带宽内,环路对输入是存在一定的衰减的,这就意味着我们的环路对输入信号有低通滤波的特性。
为了消除这种滤波的特性(差分特性),Inose在1962年将积分器由反馈路径移动至前馈路径上,就产生了我们希望的DSM,即Delta-Sigma Modulator,如下图所示,
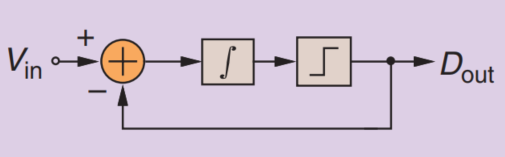
其输入传输函数如下所示,
$$
H_{CL}=\frac{H_{sum}}{1+H_{sum}}=\frac{A}{s+A}
$$
可以看到,在低频处,系统的输入基本没有衰减,在$\omega>A$的带宽处,开始以$20dB/dec$的速度进行衰减,所以,只要我们的输入信号是一定的低频信号,我们就不会破坏输入信号。
一阶数字DSM
如下图所示,下面的两张图中的左图表示了数字DSM的硬件实现图,右图表示了数字DSM的z域系统框图。
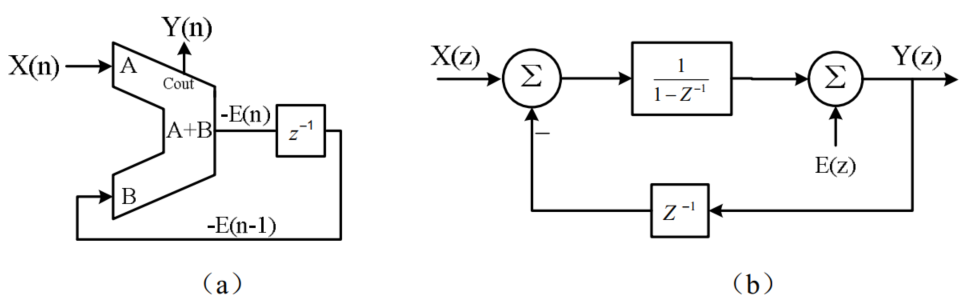
左图中的数字DSM的硬件实现图中,有两个器件组成:1. 全加器。2. 延时单元(寄存器)。这两个器件共同构成了DSM的硬件实现。我个人从DSM的本质可以解释一下这个硬件实现,DSM的本质是算出与目标值的差,再将本次的差留存到下一次累加到结果中,根据这种描述,这个差实际上就是全加器的结果$-E(n)$,经过一个触发器给到下一次的运算。至于这里的负号的原因是因为为了和右侧的线性模型中的符号对应,在右侧的线性模型中,$Y(z)=E(z)(1-z^{-1})+X(z)$,左侧对应的表达式就是 $Y(n)+(-E(n))=X(n)+(-E(n-1))$。读者仔细分析一下就可以明白其中的道理了,上述说法也自然说明了左右两个模型是完全等价的。
一阶数字DSM的噪声频域特性
在一阶数字DSM中,噪声的来源主要是$E(z)$,该噪声经过环路整形$1-z^{-1}$之后,会获得一个新的噪声曲线,现在分析环路的噪声频率特性。
$$
H_E(z)=1-z^{-1}
$$
上述表达式描述了环路的噪声传递函数,根据$z$变换与$\omega$变换的等价变换,
$$
z=e^{sT_s}=e^{j\omega T_s}
$$
其中,$T_s$为采样周期,根据上式有如下表达式,
$$
H_E(\omega)=1-e^{-j\omega T_s}=1-cos(-\omega T_s)-jsin(-\omega T_s)$$
进一步化简有,
$$
H_E(\omega)=1-cos(\omega T_s)+jsin(\omega T_s)
$$
由于我们需要求解函数的噪声功率的传递函数,所以我们对上式进行取模平方操作,有,
$$
|H_E(\omega)|^2=(1-cos(\omega T_s))^2+sin^2(\omega T_s)=2-2cos(\omega T_s)
$$
根据倍角公式,$sin^2\alpha=\frac{1-cos2\alpha}{2}$,有,
$$
|H_E(\omega)|^2=2-2cos(\omega T_s)=4sin^2(\frac{\omega T_s}{2})
$$
所以读者可以看到一阶的DSM的噪声传递函数是一个二次sin函数的1/4,低频处增益低,高频处增益高。下图将$4sin(\frac{2\pi x}{20})$绘制了出来
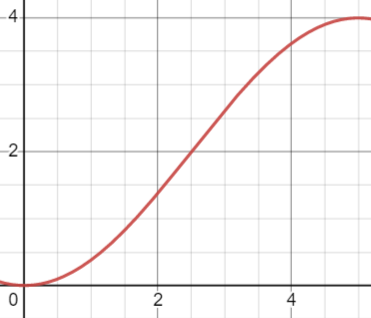
从上图中可以看出明显的NoiseShaping效应,这里的Nyquist频率为$\frac{f_s}{2}=5$,假设$f_B$为信号频率,过采样率定义为如下,
$$
OSR=\frac{f_s/2}{f_B}
$$
曲线下方的面积与$M^3$成正比。
DSM的杂音问题
假设$Vin=0.001V_{ref}$,那么$D_{out}$的输出就为1个1和999个0,这样循环周期重复,假如有足够的样本,就会有杂音落在我们的信号带内,导致出现额外的杂散,可以采取dithering打散这种周期性,将这些杂音变到我们的噪底上。
高阶DSM
高阶DSM的框图如下所示,
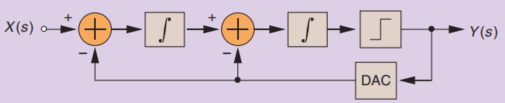
高阶DSM对于输入来说是没有影响的,但是每增大一个DSM的阶数,就会在噪声上乘以一个$(1-z^{-1})$的系数,对噪声进行整形。

