写在前面
本文内容来自于
“R. B. Staszewski, C. Fernando and P. T. Balsara, “Event-driven Simulation and modeling of phase noise of an RF oscillator,” in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 52, no. 4, pp. 723-733, April 2005, doi: 10.1109/TCSI.2005.844236.”
我本人在做ADPLL的仿真时，在对jitter进行建模时，不清楚jitter的作用机制是怎么样的，并且也不清楚按照简单的正太随机数叠加在频率上，到底对最终的相位噪声又怎么样的影响。所以，希望通过这篇文章理清这其中的逻辑和机制，之后在面对抖动建模问题时，至少有一个思考的方向和思路。
DCO的一些噪声来源
为什么使用VHDL而不是使用Verilog？
作者给出的解释时VHDL支持实数（浮点数）类型的信号，由于通信里面信号有些是在幅值上是连续的，所以使用VHDL能够对这类型号做更好的建模。
所以作者选择了VHDL对整个模型进行仿真，原因如下，
- VHDL相比于SPICE或者analog mixed-signal VHDL(VHDL-AMS)更加快速
- VHDL相比C、MATLAB等环境能够与硬件形成比较好的关联和匹配，而不是像C、MATLAB一样是一种高层次的行为模型，与硬件完全割裂开来。
基本的一些时域等式
我们假设$f_o$为我们的标称振荡频率，换句话说也就是我们的理想震荡频率，定义$T_o=\frac{1}{f_o}$为我们的理想震荡周期。
定义$\Delta T$为时钟周期减少的量，那么定义新的时钟周期如下，
$$
T=T_o-\Delta T
$$
新的时钟周期的变化一定为导致标称频率$f_o$发生$\Delta f$的变化，那么新的震荡频率如下所示，
$$
f=f_o+\Delta f
$$
如果我们的周期变化的长度远远小于我们的时钟周期$\Delta T << T_o$，即$\frac{\Delta T}{T_o}<<1$，那么我们可以得到如下的周期变化量$\Delta T$与频率变化量$\Delta f$之间的关系，
$$
\Delta f\approx f_o\frac{\Delta T}{T_o}=f_o^2\Delta T=\frac{\Delta T}{T_o^2}
$$
上述式子表明，在$\Delta T$非常小的时候，可以认为$\Delta T$与$\Delta f$之间是线性关系，以中心频率的平方为斜率。
频偏与时偏线性关系的推导
下面推导一下上面的结论，
$$
f_o+\Delta f=\frac{1}{T_o-\Delta T}=\frac{1}{T_o}\frac{1}{1-\frac{\Delta T}{T_o}}=f_o(1+f_o\Delta T)
$$
上面的式子成立的原因是$\frac{1}{1-x}$的泰勒展开，
$$
\frac{1}{1-x}=1+x+x^2+x^3+···+x^n+o(x^n)
$$
所以，
$$
\frac{1}{1-\frac{\Delta T}{T_o}}=1+\frac{\Delta T}{T_o}
$$
证明完毕。
相位噪声的时域建模
作者这边先给出了振荡器的相位噪声的频域模型，如下图所示，
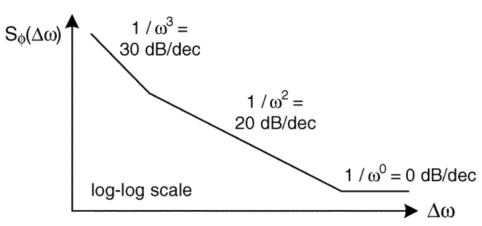
这边三段曲线代表了不同的来源的相位噪声，第一段$1/\omega^3$和第二段$1/\omega^2$应该比较熟悉了，第一段是$1/f$噪声造成的；第二段是热噪声造成的。第三段可能大家平时不会去关注，是由于输出buffer等造成的噪声。
作者把这两种相位噪声造成的时钟在时域内的时间戳的偏差分类为：
- jitter
- wander
作者给几个区域的时域时间戳偏移下了定义：说$1/\omega^0$的区域为非累积性jitter；$1/\omega^2$的区域为累积性的wander；$1/\omega^3$的区域为多种wander贡献的加权和。
上述描述还是非常不明确，什么是jitter？什么是wander？读到这里我会有这些疑问。
振荡器Jitter的建模
这里作者先从最右侧曲线的$1/\omega^0$的部分开始建模，作者先给出了下图，下图描述了该部分造成的nonaccumulatitve jitter，那么什么是nonaccumulative jitter???
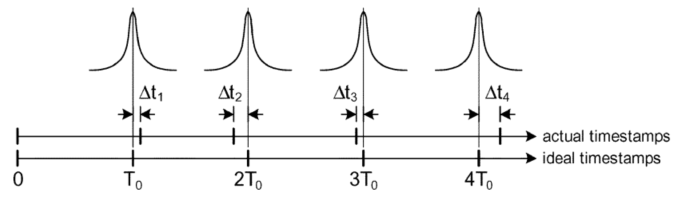
图片下方的刻度$T_0$的整数倍，表示了理想等间距(equidistant)的工作在$f_0$的时钟的上升沿时刻。这里的抖动的成因作者说是因为输出的实体buffer造成的，这句话可以理解；作者又说这些时间误差将会叠加在每一个理想的时间戳出现的时刻上。到这里我大概能明晰了，因为这种抖动不是振荡器形成时钟的时候产生的，所以并不会影响到周期，当前时刻的抖动也不会对下一个时刻的抖动产生影响。（这句话并不是作者说的，只是我自己的猜测）哈哈，果然，马上作者就说了：”These timing errors do not influence one another. “。这句话直接印证了我的猜测。
那么分析了这么多，这种噪声应该如何进行建模呢？作者说这些抖动都是独立同分布的，可以使用Additive White Gaussian Noise(AWGN)进行建模。
作者为了更加清晰地，没有歧义地描述这个问题，马上给出了这个时间戳偏移的数学表达式，如下所示，
$$
t_j[i]=i\cdot T_0 + \Delta t[i]\
TDEV_j[i]=\Delta t[i]
$$
所以可以看到偏移完全是独立同分布的服从正态分布的随机变量，补一个插曲，这里又和我研一的时候选修的随机过程建立了关联，我记得这种独立同分布且服从正态分布的随机过程为布朗运动。
作者马上给出了一个推论period deviation，周期偏移，的方差为时间戳偏差的两倍，因为$p_1[i]=t_j[i]-t_j[i-1]=T_0+\Delta t[i]-\Delta t[i-1]$，因为两个$i.i.d.$的随机变量的方差对加法和减法都是加倍。
根据上述描述，作者给出了如何计算该种时间戳偏移的均方根值得方法，作者将这个量称为rms jitter, $\sigma_{\Delta t}$。具体的计算公式如下，
$$
\sigma_{\Delta t}=\frac{T_0}{2\pi}\cdot\sqrt{\mathcal{L}\cdot f_0}
$$
其中，$\mathcal{L}$表示了相位噪声功率的双边谱密度。可以看到这个式子和我们之前使用的积分再转换的计算均方根的抖动的公式是一样的，如果不熟悉的读者可以再回去看看我的”ADPLL相位域MATLAB模型”一文。
作者还给了一个例子，说了典型值大概为$\sigma_{\Delta t}=33fs$，如下所示，
振荡器Wander的建模
作者又对热噪声引起的Wander进行了建模，这里终于要开始解决Wander和Jitter的区别了。作者说这种wander属于accumulative jitter，属于累积性的。这个其实从噪声源的本质也可以理解，这个噪声是产生于决定时钟周期的过程中的，（时钟内部），换句话说，这个噪声一定程度上是时钟周期诸多变量当中的一个。作者说，当前的时间戳还取决于先前噪声的综合；作者还说，这种行为被建模为随机游动（随机过程中的概念，真希望之前好好学习随机过程）。
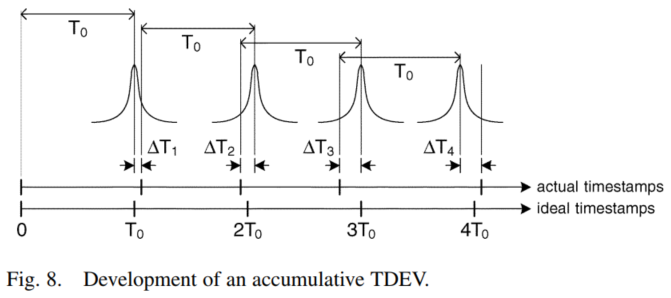
同样的，为了避免混淆，作者马上给出了Wander的数学表达式，
$$
t_w[i]=i\cdot T_0+\sum^i_{l=1}\Delta T[l]\
TDEV_w[i]=\sum^i_{l=1}\Delta T[l]
$$
可以看到这里和jitter的区别在于存在一个累加的操作，而jitter的$TDEV$是与先前噪声样本无关的。
这里作者给出了$\Delta T$的rms值得公式，如下所示，
$$
\sigma_{\Delta T}=T_0\cdot\Delta\omega\sqrt{\frac{\mathcal{L}{\Delta\omega}}{2\pi\omega_0}}=\frac{\Delta f}{f_0}\cdot\sqrt{T_0}\cdot\sqrt{\mathcal{L}{\Delta\omega}}
$$
注意，这里求的抖动不是$TDEV_\omega$的均方根抖动，而是$\Delta T$的均方根抖动。所以这里就是我一直产生问题的地方，这个$\sigma_{\Delta T}$求出来其实非常小，大概只有几个$fs$但是造成的$jitter_{rms}$其实是挺大的。
Wander标准差的推导
本文作者对于这个公式给出了两个引用，分别是：
- [9] T. C. Weigandt, B. Kim, and P. R. Gray, “Analysis of timing jitter in CMOS ring oscillators,” in Proc. IEEE Solid-State Circuits Conf., vol. 4, Jun. 1994, pp. 27–30.
- [10] A. Zanchi, A. Bonfanti, and S. Levantino et al., “General SSCR vs. cycle-to-cycle jitter relationship with application to the phase noise in
PLL,” in Proc. Southwest Symp. Mixed-Signal Design, Feb. 2001, pp. 32–37.
上述两个引用都没有对这个公式的推导，在[10]引用中，作者A. Zanchi et al.描述了这个公式的来源，在[10]引用一文中的[1]引用中：
“C. Samori, A. L. Lacaita, A. Zanchi and F. Pizzolato, “Experimental verification of the link between timing jitter and phase noise”, IEEE Elec. Lett., vol. 34, no. 21, pp. 2024-2025, Oct. 1998.”
在这篇文章中，作者对该内容进行了详细的推导，现将我理解的推导过程列为如下，
在PLL中，频率谱与相位谱的关系如下所示，
$$
\begin{equation}
S_{f_o}(f_n)=f_n^2S_\phi(f_n)
\end{equation}
$$
假设我们的时间抖动远远小于我们的时钟周期，有下式成立（此式常用，已经在本人博客多篇相关文章中描述过），
$$
\begin{equation}
\Delta f_o=-\frac{\Delta T_o}{T_o^2}=-f_o^2\Delta T_o
\end{equation}
$$
由式（2）我们可以得到下面的表达式
$$
\begin{equation}
\sigma_{f_o}^2=f_o^4\sigma_{T_o}^2
\end{equation}
$$
这里我们假设我们的独立振荡器只有热噪声，那么其频率谱可以表示为一个平带热噪声，双边噪声功率谱密度为$S_{f_o}(f_n)$，那么我们可以得到频率方差如下，
$$
\begin{equation}
\sigma_{f_o}^2=f_o\cdot S_{f_o}(f_n)
\end{equation}
$$
再将式(1)代入式(4)，有，
$$
\begin{equation}
\sigma_{f_o}^2=f_o\cdot S_{f_o}(f_n)=f_of_n^2S_\phi(f_n)
\end{equation}
$$
再由式(3)得到下式的关系，
$$
\begin{equation}
\sigma_{f_o}^2=f_o^4\sigma_{T_o}^2
\end{equation}
$$
将式(5)与式(6)整理可以得到，
$$
\sigma_{T_o}^2=\frac{f_n^2}{f_o^3}S_\phi(f_n)
$$
需要注意的是，上式成立的条件是：
- $\sigma_{T_o}$足够小；
- $S_{f_o}(f_n)$为平带的白噪声。
如果2条件不成立，那么我们可以参考文献：
E. J. Baghdady, R. N. Lincoln and B. D. Nelin, “Short-term frequency stability: Characterization, theory, and measurement,” in Proceedings of the IEEE, vol. 53, no. 7, pp. 704-722, July 1965, doi: 10.1109/PROC.1965.3995.
该文献给出了频谱与timing jitter之间的关系。
仍需要注意的是，这里的抖动指的是短期抖动，并不是长期抖动，与我们的所认知的长期抖动是不符合的。（这是我自己的认知，不知道是否正确）
wander的例子
在我们的应用中，中心频率为$f_o=30GHz$，周期为$T_o=33.3ps$，在频偏@$\Delta f=610.87kHz$，相位噪声功率谱密度为$\mathcal{L{\Delta f}}=10^{-101.38/10}=7.27\cdot10^{-11}rad^2/Hz$，最后计算出来的$\sigma_{\Delta t}\approx1fs$
如何根据时间戳给出相位噪声功率谱密度？
我先暂时略去了作者关于$1/f$噪声建模的描述、以及作者对振荡器VHDL代码的描述。目前还没有考虑到这一步。作者对于测绘振荡器时间戳的相位噪声功率谱密度相关的内容是非常有意义的。时间戳的绝对值的偏移是我们用来计算的量，为了避免混淆，在这里给出数学表达式，这个量的数学表达式如下所示，
$$
TDEV[i]=t[i]-i\cdot T_0
$$
作者这边说，”Relationship between $TDEV$ and phase noise $\phi$ is straightforward: $\phi[i]=2\pi(TDEV[i]/T_0)$.”。实际上这个关系就是我们常用的如下的数学关系，直观上理解就是横坐标变化量$\Delta t$乘以斜率$2\pi f_0$等于纵坐标变化量$\Delta\phi$。
$$
\Delta\phi=2\pi f_0\Delta t
$$
直接对上述转换后的数据进行$FFT$操作就可以得到我们的幅度谱频谱了，平方后得到功率谱，再除以我们的频谱分辨率$f_{res}$就可以得到我们的噪声功率谱密度了。
至此，我认为作者已经完整描述了如何使用VHDL进行建模并且如何进行结果分析的流程，接下去就等着我进行复现和实践了！！
